Who should win with this simple set of cardinal ballots?
-
Here are some cardinal ballots, rated 0-5. Under Score and STAR, it is a 3 way tie. They are tied in terms of pairwise wins.
a[5] b[0] c[0] a[5] b[0] c[1] a[5] b[0] c[2] a[0] b[5] c[3] a[0] b[5] c[4] a[0] b[5] c[5]Candidates A and B both have only 0s and 5s. C has one of each rating.
Are they all equal, or are some better choices than others?
And yes @cfrank this is a bit inspired by the consensualism concept.
-
@rob interesting puzzle, my intuition/weak opinion is that C should win this election somehow, since C seems somehow less divisive than A or B. I think it would be interesting to look at ballots like this and have a vote as to who should win based on the ballot.
Not that this is important, but choosing C is also consistent with SP Voting with the 1/2-geometric weighting, where the distribution is discrete and determined by the ballots directly.
C gets a “fitness metric” of
(2/3)(1/2)+(2/3)(1/4)+(1/3)(1/8)+(1/3)(1/16)=0.5625
while A and B both get metric of
(1/3)(1/2)+(1/3)(1/4)+(2/3)(1/8)+(2/3)(1/16)=0.375
With a STAR runoff based on these metrics, I believe C should still be selected since the majoritarian runoff is indeterminate.
I think most proposed concave score systems would come to the same result. I don’t know if that’s a satisfactory justification, since an alternative ballot set could probably be constructed to be indecisive in those systems as well. Which candidate would you vote for? Or do you think this case is essentially the score-analogue of a Condorcet cycle, and the winner might as well be chosen at random?
One system I also like in principle is called Bucklin Voting. We can try to apply the Bucklin procedure using scores rather than ranks, and C is also the Bucklin winner.
Simpson Voting (Maximin) depends on how ties in preference are counted. If a tie is counted as positive, then B and C are both Simpson winners. Otherwise it’s indeterminate.
A completely different approach would be to use Young Voting and determine the smallest number of ballots that need to be removed to make each candidate a strong Condorcet winner (weak winner is indeterminate). We can make A a strong Condorcet winner by removing a single ballot, namely the bottom one. However, I don’t think we can make B or C a strong Condorcet winner with fewer than two ballot removals. So Young Voting based on weak rank order preferences would elect A.
I would like to see what Dodgson voting does, but the mechanism requires an analogue for scores and/or weak rankings.
-
@cfrank I agree that C seems to be a less divisive candidate, and given that everything else is equal, you can test for "average deviation" (or I guess standard deviation, I didn't bother), and measure the divisiveness in a sense.
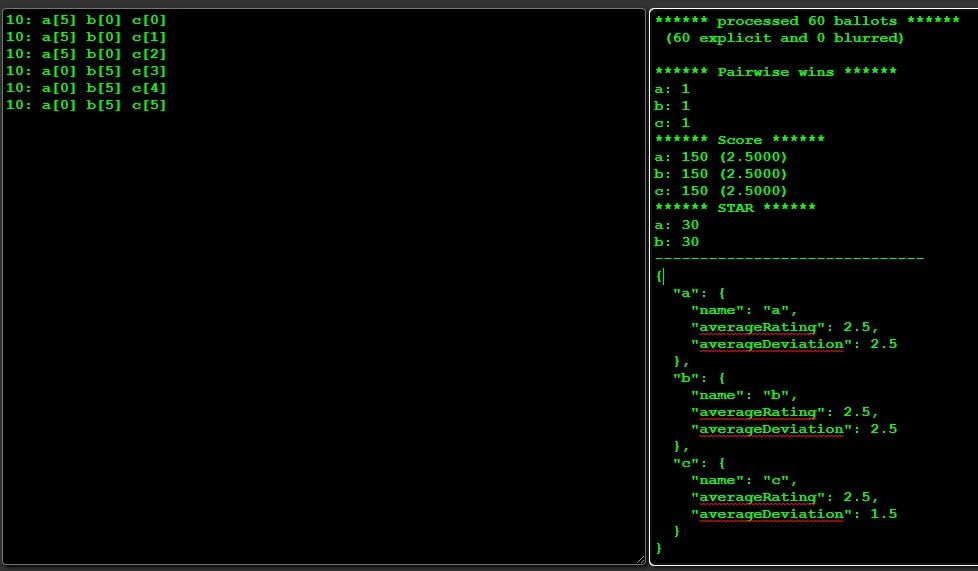
https://codepen.io/karmatics/pen/NWvLozE
Seems like in the case of pairwise tie this might be a reasonable tiebreaker.
-
@rob that seems reasonable to me. A long while ago I was trying to consider score distribution metrics of the form
Avg*F(Stdev/Avg)
where F is a decreasing function (probably exponentially) and F(0)=+1. The metric scales directly with the distribution, but it’s only sensible for scores that aren’t negative unless you do a canonical shifting by the minimum score. It might also be considered a bit haphazard and computationally obnoxious, since standard deviations are annoying.
But something like
Avg/2^(Stdev/Avg)
would elect C.
If there was a faster formula to get a decent measure of the spread, that would be nice. Possibly the IQR or some other quantile range could be a substitute, and we would have
Avg/2^(IQR/Avg)
or we could possibly involve the median as well somehow.
The ratio Stdev/Avg is also known as the coefficient of variation. Apparently there is another more robust measure of dispersion that is very easy to compute: https://en.m.wikipedia.org/wiki/Quartile_coefficient_of_dispersion
QCD=(Q3-Q1)/(Q3+Q1)
Something like the metric
Avg/2^(QCD)
could possibly be applicable.
-
While people aren't likely to cast votes that are perfectly related to utility, I still see scores as more akin to utility than to something like money, where the increase in utility drops off the higher up the scale you go.
So what I'm saying is that I see a 5 and a 0 as in the same ballpark as a 3 and a 2, rather than the 3 and 2 being preferable for equity reasons.
How good score voting is generally is a separate debate obviously, but where it gives the same tie as a pairwise method, I don't see any reason in principle to prefer one result over another. But as a tie-break, it's probably fine to choose the result you might consider less divisive.
An interesting follow-up question would be whether you would consider divisiveness over score where there isn't an exact score tie (but is a pairwise tie still) or whether it's only useful as a tie-breaker. You could, for example, reduce C's score of 3 to 2. That way, the pairwise result is still a tie but on average scores, A and B are now marginally ahead of C despite being more divisive. Is there still an argument to elect C?
-
If you randomly remove one ballot, then A wins in 3 of 6 possible cases, B wins 2 of 6, and one is a B-C tie.
I have no opinion on who should win. For me this is just a 3-way tie.
-
@toby-pereira surely there is an argument, which is that the degree of divisiveness of A and B somehow diminishes their overall fitness for election below the fitness of C. Formalizing that argument requires specifying how fitness is being measured and how it incorporates a measure of divisiveness.
If you use some metric as I describe just above, you arrive at one specific decision procedure that formally incorporates that sort of reasoning. I think something along those lines with some sort of STAR-like runoff could be a good system.
-
@toby-pereira said in Who should win with this simple set of cardinal ballots?:
An interesting follow-up question would be whether you would consider divisiveness over score where there isn't an exact score tie (but is a pairwise tie still) or whether it's only useful as a tie-breaker.
Personally I would consider this a reasonable way to deal only with pairwise ties (i.e. no Condorcet winner). I'm not even convinced on that, since for me game theoretical stability is prime importance.
But still, if you are going to try to increase the likelihood of non-divisive candidates being elected, which I think is a noble goal (and, if I'm not mistaken, is something @cfrank has stated as a goal), something like this where it tries to measure divisiveness directly is worth looking into. For instance, if given a choice between picking the highest scoring candidate from the Copeland or Smith set, vs. picking the one with the lowest average deviation, I think I'd go with the latter.
-
@rob I think it would also be interesting to get votes on what forum users consider the most important aspects of a voting system.
It would also probably be useful to get some kind of informal map of different voting systems plotted on a spectrum of relative characteristics. I think a triangular spectrum of stable vs. simple vs. consensual could be a good place to start.