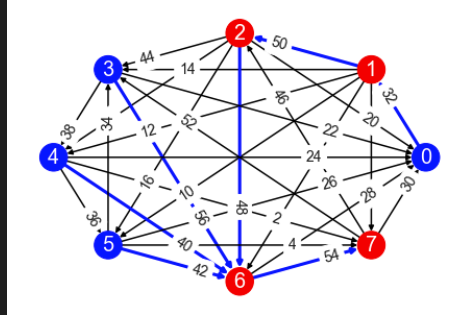
A Graph Theoretical Conjecture
-
Say I have a tournament graph G = (V, E) where every edge has a unique positive weight, and I have a function f: V --> V with the following property:
- E contains (x, f(x)) for all x
And, for all y, and z != y, f(y), then either:
- E contains (f(y), z), or
- There is a path in G from f(y) to z such that each edge has larger weight than (z, f(y))
Now let x be such that (x, f(x)) is minimized. Must there be a path in G from f(x) to x where each edge has a larger weight than (x, f(x)) ?
Any insights, proofs, or counterexamples welcomed. I've been thinking about this problem for a while now.
-
This post is deleted! -
@brozai Here is a basic detail. In any counterexample, f cannot be a single cycle, since when we take x such that (x, f(x)) is minimized, we can take the path from f(x) to x, f(x) -> f^2(x) ->... -> f^|V|(x)=x.
Edit: If we take x such that (x,f(x)) is minimized, we can get a path from f(x) to x by repeatedly applying f and using the edge (f^i(x), f^i+1(x)). Since (x,f(x)) is minimal all of these edges will have weight higher than (x,f(x)). ((x, f(x)) will never have to be used because once x is reached, we're done.)
We are guaranteed to reach x because f is a permutation and permutations can always be decomposed into disjoint cycles. -
Hi @marylander , thank you for taking the time to think about this problem.
This is a good observation. You can construct such a graph where f creates a a single cycle by, for example, having a Hamiltonian cycle consisting of all the strongest edges in E.
Unfortunately, f may not be injective, so it will not necessarily be a permutation. I believe, however, that we can reduce to the case where f(x) (for specifically the x as chosen to minimize (x, f(x)) has a unique preimage
-
@brozai True. Then this only shows that in any counterexample f cannot be a permutation/injective.
-
@marylander Here is an example graph which is quite annoying, in that it shows it is possible to construct such a graph where f is not a permutation
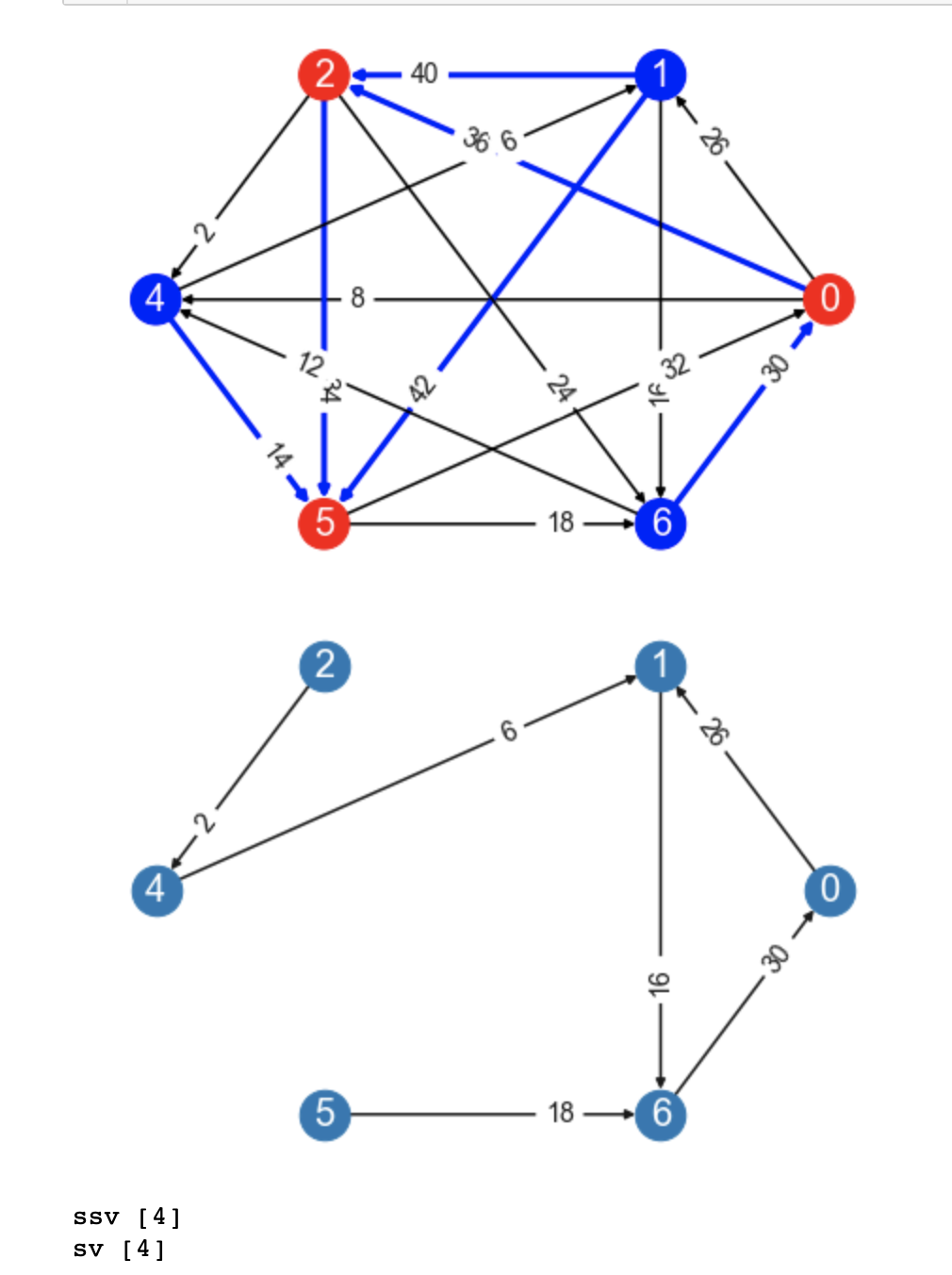
The bottom graph shows the edges selected by f
-
@brozai I think I found a counterexample
From c1 c2 c3 l0 l1 l2 b1 b2 d1 c1 - -98 - - - - - - - c2 - - 4 - - - - LO - c3 LO - - 2 - - 13 12 - l0 -99 1 - - -10 - - 9 - l1 LO LO LO - - -11 -8 LO - l2 LO LO LO -13 - - - 20 - b1 LO 3 - -7 - -9 - - - b2 LO - - - - - 8 - -96 d1 LO LO LO -97 LO LO LO - - f(c1)=c2 f(c2)=c3 f(c3)=l0
f(l0)=l1 f(l1)=l2 f(l2)=l0
f(b1)=l0 f(b2)=d1
f(d1)=l0Edit: at the end of the row for l0, changed the last 3 values from 9/-7/- to -/9/-
Also changed the edge from l2 to b1 with weight -12 to an edge from b1 to l2 with weight -8. -
Hi @marylander ,
This is a great find, but remember all the edge weights should be unique! Nonetheless it's interesting to know that the conjecture does not hold in general.
Edit: Also, is there both an edge (l0, b1) and (b1, l0) ? I may be misinterpreting
Btw if you're curious for context, this is related to a question in https://arxiv.org/abs/2108.00542 that Simple Stable Voting will return a candidate in the Split Cycle set over uniquely weighted tournaments.
-
@brozai Sorry, I made a transcription error. I can upload the sketch I based the matrix on, although it is jank. At first I didn't upload it because I didn't think it would be readable adding the LO edges.
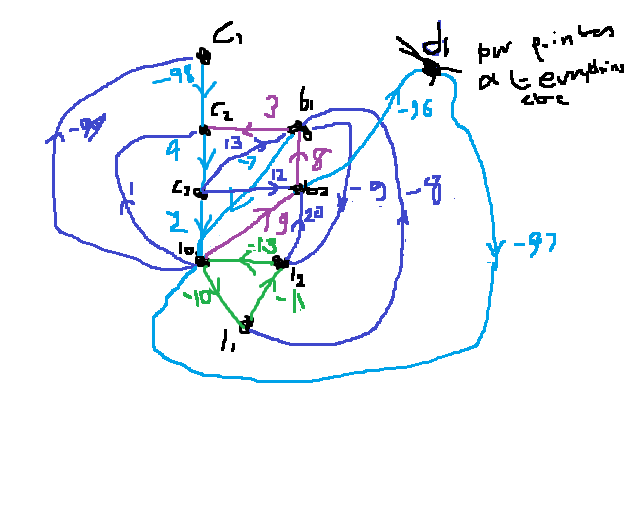
I tweaked the example slightly as well but I don't think it was necessary.
-
@marylander Thanks yup, this looks like a counterexample.
Using some of the ideas in your construction I found a slightly smaller one on 8 nodes