This paper was posted a few weeks ago: Moderation in instant runoff voting

In this work, we prove that IRV has a moderating effect relative to traditional plurality voting in a specific sense, developed in a 1-dimensional Euclidean model of voter preferences. Our results show that as long as voters are symmetrically distributed and not too concentrated at the extremes, IRV will not elect a candidate that is beyond a certain threshold in the tails of the distribution, while plurality can.

This is certainly true, as they frame it. There is an extreme region of the political spectrum where FPTP will elect candidates that IRV doesn't:

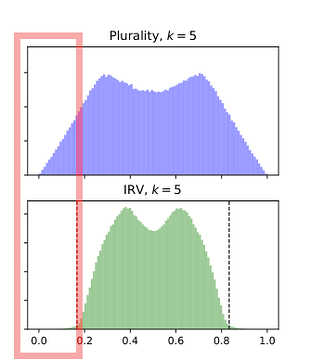
But it's a bit weird of a claim to make, since IRV is still pretty broad, and has that valley of anti-moderateness in the middle, and other voting systems do much better. They acknowledge this to some extent, saying they focus on IRV because it's the only system with momentum:

First, we are not trying to characterize all possible voting systems that have a moderating effect under our formal definition, and if our goal were simply to design a voting system that has a moderating effect, there are many additional systems not in wide use that exhibit this property (any Condorcet method, for instance, or the Coombs rule [7, 22]). Our interest, instead, is in the fact that IRV and plurality are both used extensively in practice, and that they differ in this key property: IRV has a moderating effect and plurality does not.

Finally, as we noted earlier, there are voting systems that always select the most moderate candidate with symmetric 1-Euclidean voters. This is true for any system that satisfies the Condorcet criterion, selecting the Condorcet winner whenever one exists (this holds for the Copeland, Black, and Dodgson methods [3, 37]); it is also true for some other voting systems that do not in general satisfy the Condorcet criterion, like the Coombs rule [7, 22]. There are a variety of practical and historical reasons why these methods are not widely used for political elections. For instance, Dodgson’s method is NP-hard to compute and the Coombs rule is very sensitive to incomplete ballots, which are common in practice. As we are motivated by ongoing debates about IRV and plurality, our attention has been restricted to these voting methods. However, a broader understanding of moderating effects of voting systems would be valuable. There has been some theoretical work on moderating effects of score-based voting systems (like Borda count and approval voting) with strategic voters and candidates [11]. However, it is an open question (with some computational evidence to support it [5]) whether other voting systems like Borda count exert a moderating effect in the setting we study, with fixed voter and candidate distributions.

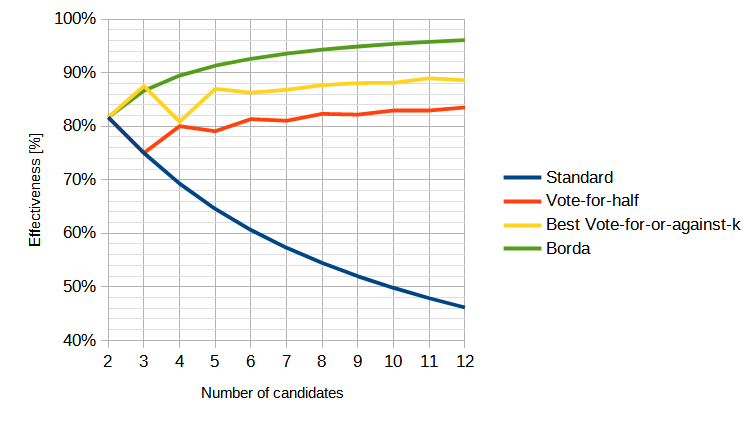
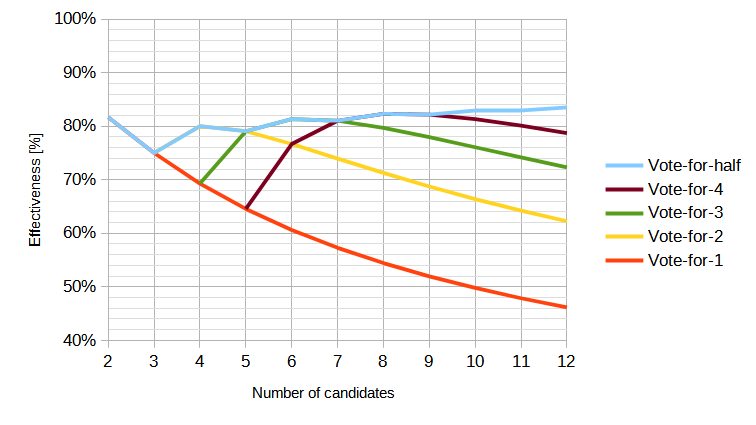
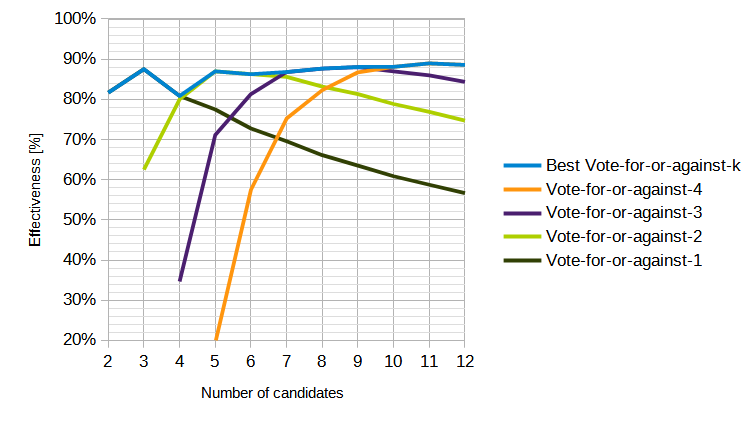
I've previously done similar simulations of other systems (though with a normal distribution of voters and candidates instead of a uniform distribution, which I think is more realistic) :

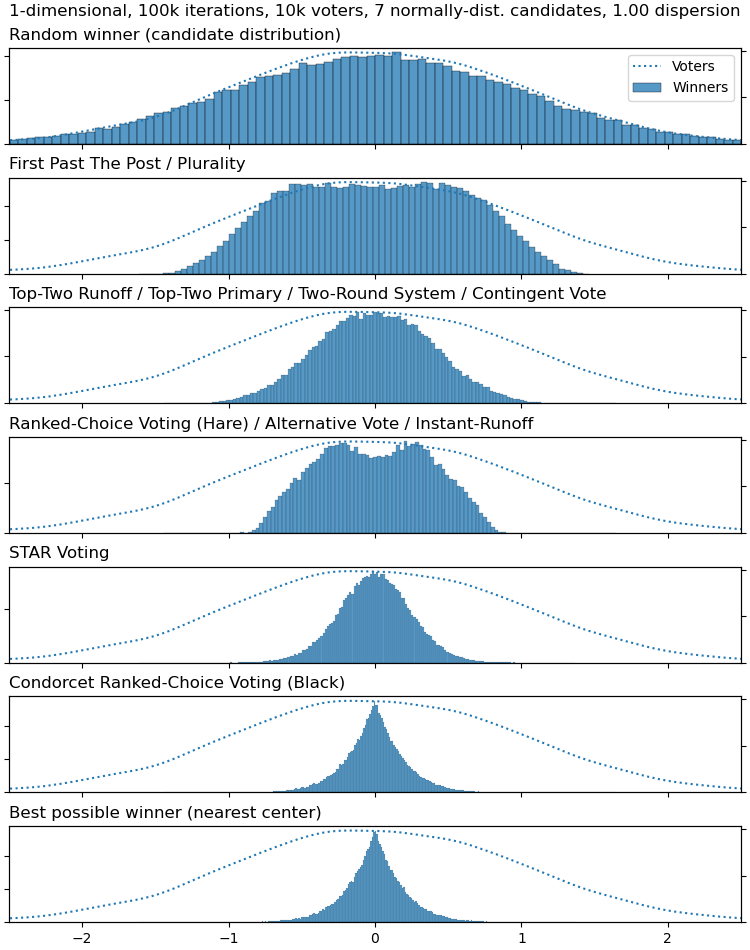
I was surprised by how similar the "first-choice only" systems behave when the candidates are clustered more tightly than the voters:

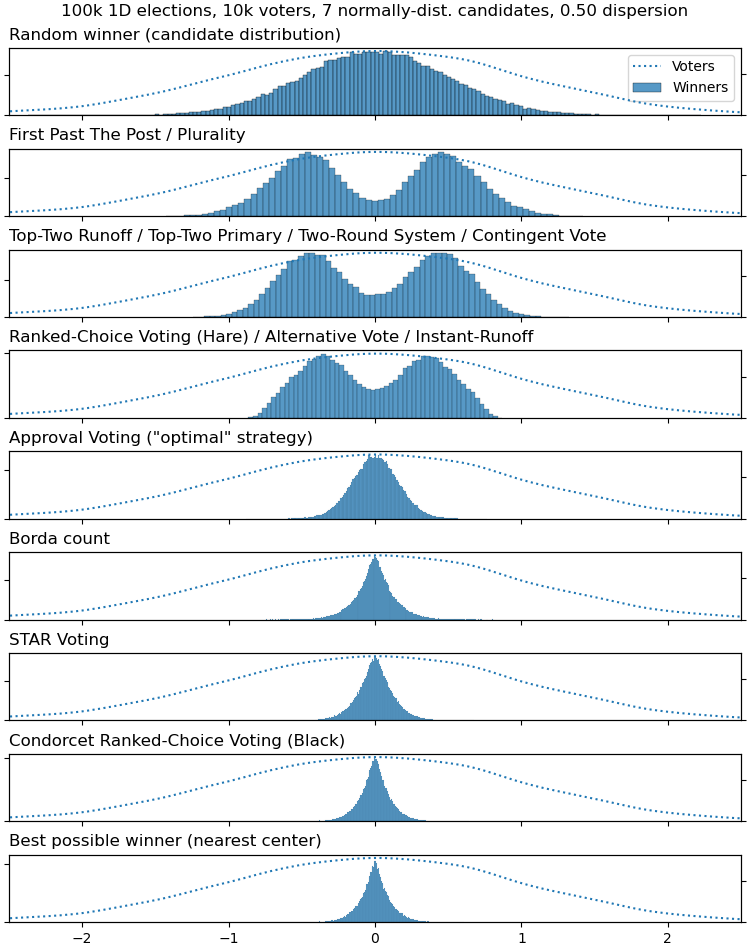
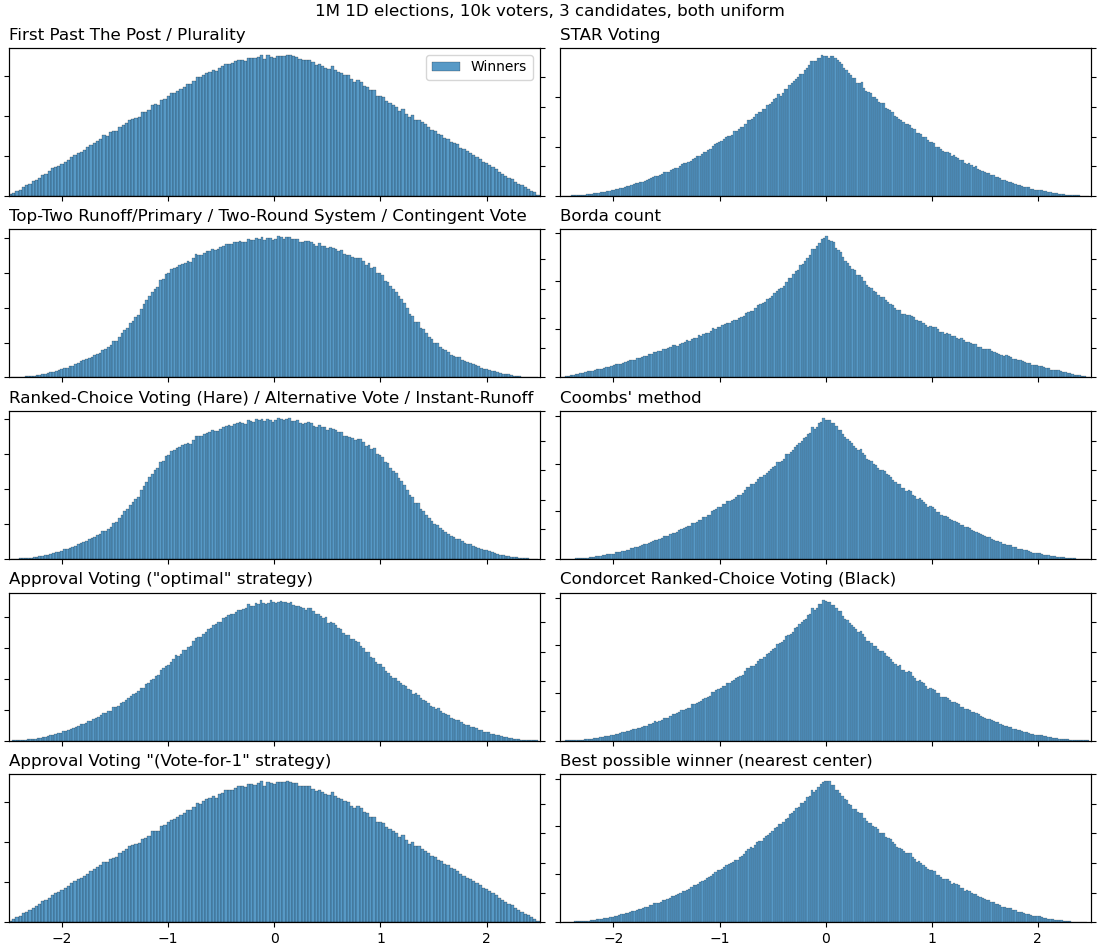
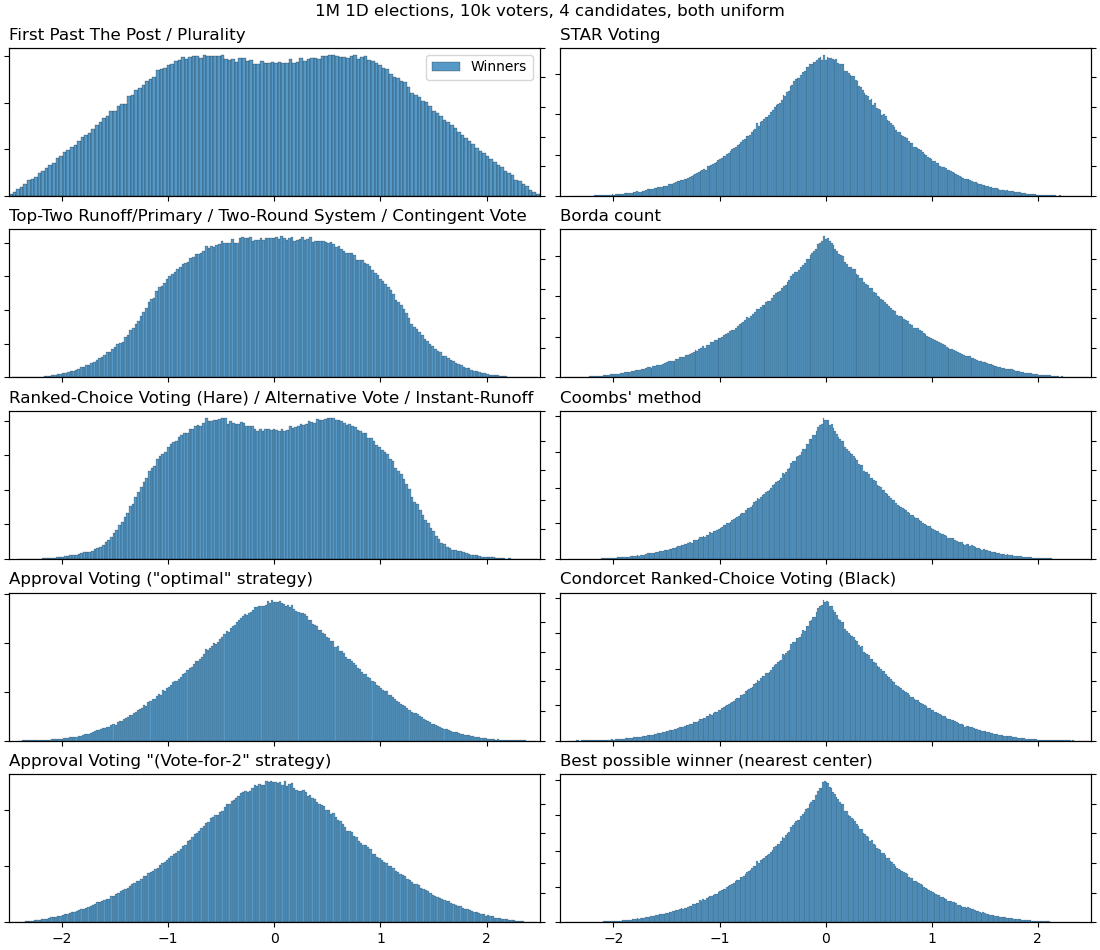
Anyway, I've tried to reproduce the graphs of the paper (with uniformly-distributed voters and candidates) but with some additional voting systems for comparison:

3 candidates:

4 candidates:

5 candidates:

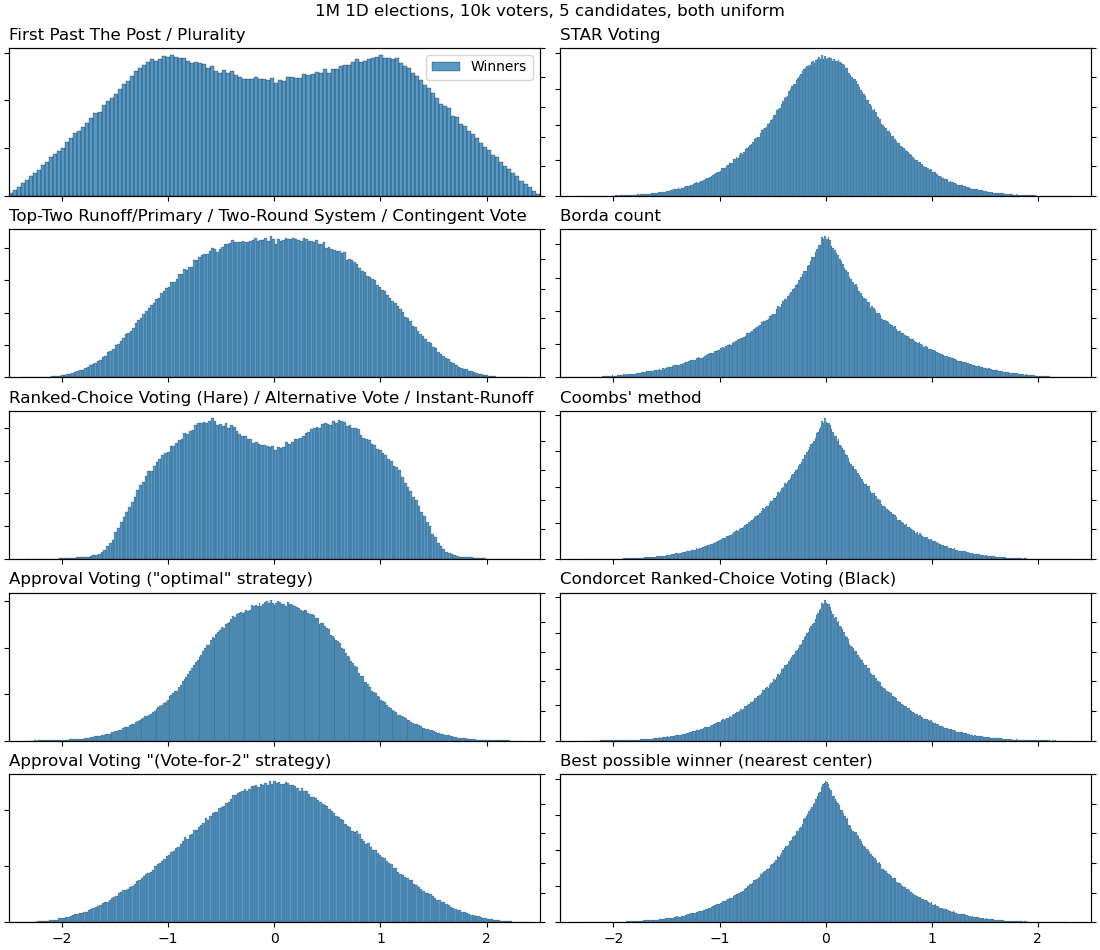
7 candidates:

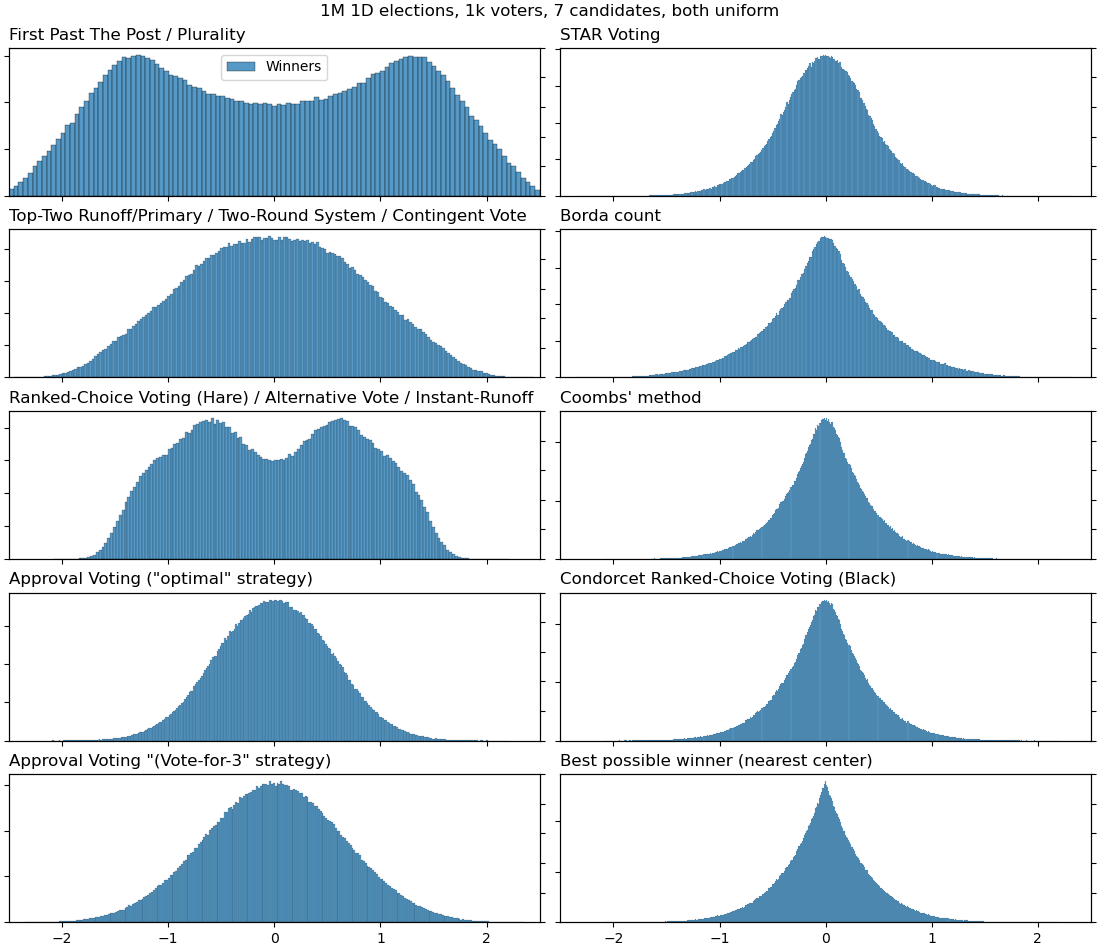
10 candidates:

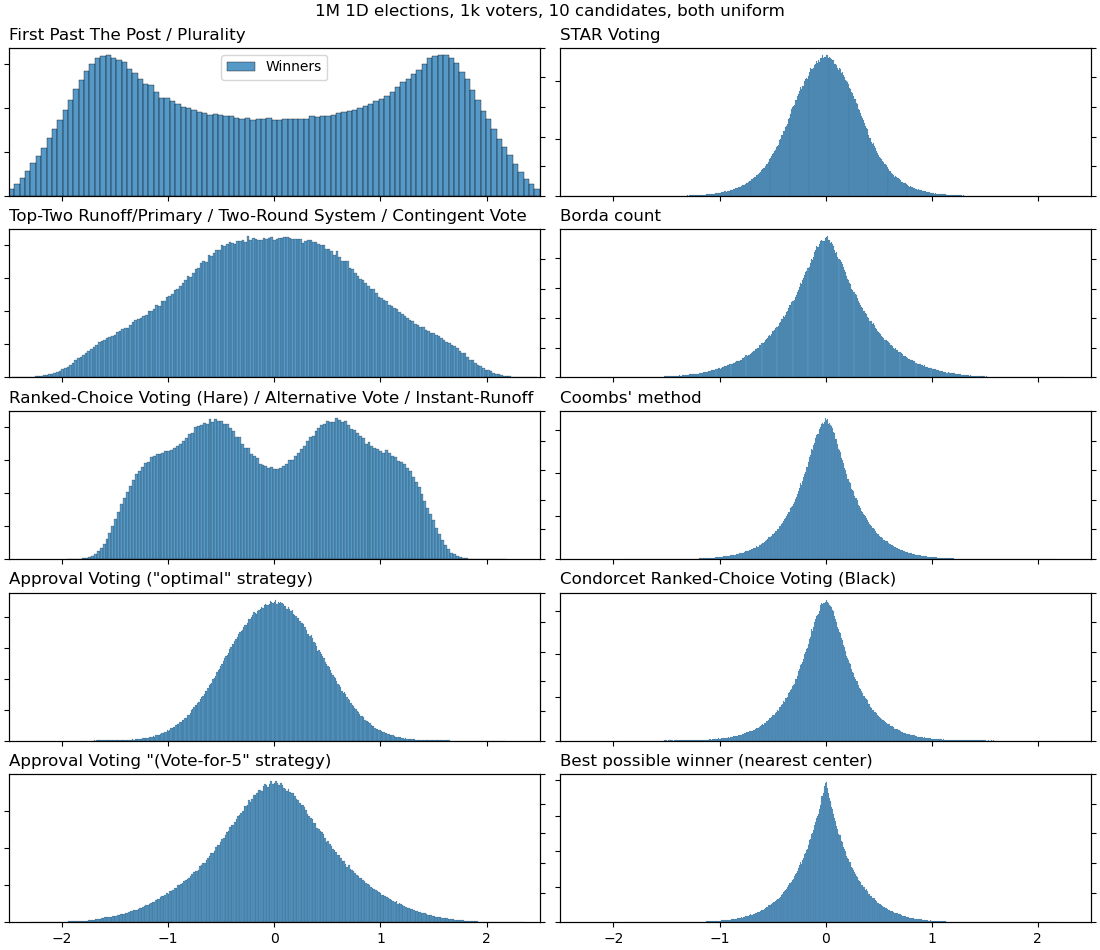
(Approval "optimal" strategy is as described in Merrill 1984: Each voter approves of all candidates they like more than average. "Vote-for-n" strategy is where every voter approves of their n most-favored candidates, from Weber 1978. STAR strategy is honest, proportional to max and min. Ranked ballot systems use honest strategy.)

From Slack:

Fellow NY'rs, action is needed! SB5259 has been placed on the calendar and would direct the state BOE to study implementing Ranked Choice Voting statewide. It needs to include STAR voting at the minimum if not more options as well. No point in a study that doesn't consider all the solutions to the problem.

Visit NYsenate.gov and Ask your senator & the sponsors (Liz Kreuger & Rachel May) to include STAR voting. We need a comprehensive study if we are going to spend public money on something this important. Feel free to leave a comment (different than sending a message) and vote Aye or Nay on this bill as you see fit (I believe you can change it later if it gets amended, I voted Aye.) You can also go further by tweeting at them if you have a twitter account.
https://www.nysenate.gov/legislation/bills/2023/s5259

In my letter I focused on the motivations mentioned in the bill:

Many advocates argue that ranked choice voting promotes consensus candidates acceptable to the largest number of voters and prevent factional candidates from winning crowded races with less than majority support.

And linked a bunch of research/articles about how the proposed method doesn't actually deliver on this promise. It would be great if a lot of other people could write them and tell them to include better methods in their study, lest we get stuck with Hare RCV.

If your senator is Republican, make sure to mention that neither FPTP nor Hare RCV (would have) worked for them in Alaska, but better consensus-focused voting methods would have won them a seat.

Cooper 2001 makes a good point about SUE vs CE:

while the concept of Condorcet efficiency permits comparison of rules, the dichotomous nature of its evaluation renders it less than perfect. To see why, consider the following example:

A population arrayed along an axis running from −10 to +10, and with a median of 0, chooses between three candidates, located at positions 1, 2, and 8. The candidate at position 1—nearest the median—is of course the Condorcet winner. Decision rule A selects the candidate at position 1 fifty percent of the time and the candidate at position 2 fifty percent of the time. Decision rule B also selects the candidate at position 1 fifty percent of the time, but the remaining fifty percent it chooses the candidate at position 8.

[Condorcet Efficiency] rates decision rules A and B as equivalent, since each selects the Condorcet candidate 50 percent of the time. Yet surely these rules differ in an important way, since rule A selects a candidate near the median—though not that nearest the median—the remaining 50 percent of the time, whereas rule B selects the most extreme candidate the remaining 50 percent of the time.

She then introduces a new metric which "resembles in spirit the concept of social-utility efficiency":

I therefore use a different measure of a decision rule's efficiency. Specifically, I adapt the concept of the Mean Squared Error (MSE) …

Although social utility involves a different calculation (the ratio between the utility of the selected candidate and that of the utility-maximizing candidate), it, like the MSE, involves not merely a ranking of candidates, but a means of capturing the intensity of voters' preferences.

But her "MSE" measurement seems pretty different in concept to me, and is still based on utility, rather than pairwise rankings/defeats like CE is.

Green-Armytage 2015 defines Utilitarian Efficiency to be analogous to CE:

In this paper we define utilitarian efficiency operationally as the likelihood that sincere voting will result in the election of the candidate who maximizes the sum of the voters’ utilities. To the extent that we view elections as a way to select the ‘best’ candidate, utilitarian efficiency is a logical criterion to consider, because maximizing the sum of utilities is a plausible operational definition of being ‘best’.

So, ignoring MSE, the other three metrics can be placed in a table:

So I've been meaning to see if there is an actually analogous metric that fills in the blank. I asked some machines (ChatGPT3.5, Bing Chat, Character.ai) a few week ago if they knew of any, and they did not, so I asked them to complete the analogy, and with some prodding they stumbled around and came up with definitions and some OK names for it.

Then when ChatGPT4 was released, I asked, and it immediately understood what I was asking, invented a metric and name, and wrote out the whole derivation:

Apologies for any confusion. I'm glad to help define this new concept. Here's a possible formula for Pairwise Ranking Efficiency (PRE):

Let's denote the following variables:

• n as the number of candidates
• W as the elected candidate in a given election
• C as the Condorcet winner (assuming one exists)
• p(x, y) as the fraction of pairwise comparisons that candidate x wins against candidate y (0 <= p(x, y) <= 1)

Now, let's define the average pairwise winning fraction for a candidate x:

APWF(x) = (Σ [p(x, y)] for all y ≠ x) / (n - 1)

The Pairwise Ranking Efficiency (PRE) can then be calculated as:

PRE = (APWF(W) - APWF_avg) / (APWF(C) - APWF_avg)

where APWF_avg is the average APWF for all candidates:

APWF_avg = (Σ [APWF(x)] for all x) / n

This formula computes the Pairwise Ranking Efficiency by comparing the performance of the elected candidate (W) with the average candidate performance and normalizing it with respect to the performance of the Condorcet winner (C). The resulting value will range from 0 to 1, where a higher value indicates better performance in electing candidates with strong pairwise ranking properties.

It's not quite right, because:

• "Fraction of pairwise comparisons" (0–1) is not the same units as n-1. Probably the (n-1) should just be dropped, because it's already a fraction? Or just use the count directly, since every term is going to be divided by the same thing anyway?
• There may not always be a Condorcet winner (to be conceptually equivalent, it should compare to the "best" candidate, even if there is no CW)

People who are more familiar with the subtleties of Condorcet systems than me: Does this make sense as a conceptual parallel?

Social Utility Efficiency (=Voter Satisfaction Efficiency) is defined as:

• (Utility(selected) - Utility(average))/(Utility(best) - Utility(average))

So for a ranking-based equivalent, we need to keep the (S-A)/(B-A) concept, but instead base it on number of pairwise defeats? So if CBB(x) = "Number of candidates beat by x", I think this is a simpler equivalent of GPT's idea?:

• (CBB(selected) - CBB(average))/(CBB(best) - CBB(average))

Or do we have to do "number of candidates beaten by x minus number of candidates that beat x" to account for ties? I don't think those are equivalent?

I've been researching the history of utility simulations, and it seems the paper that started it all is Weber 1977 (though these technically aren't simulations, since he calculated closed-form expressions analytically). Anyway, the paper isn't OCRed or bookmarked or searchable, so I had to actually skim through the whole thing with my own eyes.

Weber's "Effectiveness" is the same thing as Merrill's "Social Utility Efficiency", which is the same thing as Shentrup's "Voter Satisfaction Index", which is the same thing as Quinn's "Voter Satisfaction Efficiency": The utility of the winning candidate (totalled across all voters) , as a fraction of the distance between the average utility of all candidates (= average of many random winners) and the utility of the best candidate. For example, this winner would have a value of 75%:

--------- Best candidate

--------- Actual winner

--------- 

--------- 

--------- Average of all candidates

The paper doesn't have any graphs, just the expressions and a single table of a few Effectiveness values. I put the expressions into a spreadsheet and plotted various things, and verified against the table:

Here is The Effectiveness of Several Voting Systems table from p. 19 of Reproducing Voting Systems, except in graphical form and with more values calculated:

• Standard is of course First Past the Post, and we all know how that works.
• Vote-for-half is Approval voting, except that all voters use the identical strategy of approving half of the candidates.
  • This sounds similar, but is not the same, as Merrill's Approval strategy, in which all voters approve of any candidates of above-average utility (optimal from the voter's perspective, without any info from polls). Although this would be half approvals per ballot on average, it's not always half for an individual voter.
    • (In a quick test, it seems that the optimal strategy provides higher social utility than Weber's, but I haven't double-checked my code.)
    • (Weber does recognize that this is the optimal strategy, and says that voters using optimal strategy is assumed throughout the paper, but then … doesn't actually do that?)
• Best Vote-for-or-against-k uses the Vote-for-or-against-k method, with k set to the value that maximizes social utility for a given number of candidates (about 1/3).
  • Vote-for-or-against-k, in turn, is the method in which voters can choose to vote for k candidates, or against k candidates. So this can be thought of as combined approval voting, but with every voter using this same strategy. (I assume these strategies were used just because they were easier to calculate analytically.)
• Borda is Borda count

Weber gets a Social Utility Efficiency of 82% for all two-candidate elections, while Merrill gets 100%. This is because Merrill normalizes utilities before finding the utility winner in each election. I think Weber's approach makes more sense, since I believe that elections with polarizing majoritarian winners beating broadly-liked candidates really do happen. WDS refers to this discrepancy, too, because honest Score voting could actually get to 100%:

Note that when C = 2, achievable voting systems will not achieve zero BR. That error made in a previous study [17] probably indicates it had a computer programming “bug.”

(I think Weber mentions this, too, but assumes that everyone would normalize to min/max and so it would end up equivalent to Approval. But now I can't find it. Maybe that was another paper. I'll edit this later.)

Here's "Vote-for-k":

• Vote-for-1 is just FPTP
• Vote-for-half is the value of k that produces the best social utility for a given number of candidates, when every voter uses it, as above.

Here's "Vote-for-or-against-k":

• Vote-for-or-against-1 is the same as "negative vote" or "bipolar voting" or "balanced plurality voting".
• Best Vote-for-or-against-k is just value of k for a given number of candidates that provides the highest social utility when every voter uses it, as above.

These all use the "random society" model, so not super realistic, but still useful for relative comparisons of methods and for verifying Monte Carlo simulations against.

(I was going to transcribe the expressions here for other's convenience, but math markup doesn't work yet.)

In addition to hosting the archive of forum.electionscience.org, it would be good to host the archives of election-related Yahoo Groups (and maybe Google Groups, if CES group is going away?)

• [EM] Dumping election-methods Yahoo groups before the Dec 14 deadline
  Kristofer Munsterhjelm
• Reddit: All election-related Yahoo Groups will be deleted in 24 hours

I got some of the data from each of these, but I haven't gone through to see how complete they are:

• ApprovalVoting [Citizens For Approval Voting]
• AR-NewsWI ["Animal Right News- Wisconsin", not sure why listed]
• AVFA [Approval Voting Free Association]
• btpnc-talk [Libertarian Boston Tea Party Free Association, not sure why listed]
• Condorcet [Membership approved]
• electionmethods
• EMIG-Wikipedia [Wikipedia Election Methods Interest Group]
• instantrunoff-freewheeling
• InstantRunoffCA [Membership approved]
• InstantRunoffWI
• RangeVoting [Automatically rejected]
• stv-voting

Total size of my dumps are probably <1.5 GB with all the duplicated content removed.

Kristofer listed a few more groups that he downloaded. ArchiveTeam maybe got some that were not listed? Maybe others are floating around out there?

Unfortunately, I think some of these were lost forever, because they were accessible only to members, and no members archived them (unless they did so without posting about it).

@toby-pereira Sorry I wrote my previous short comment in line at the grocery store and forgot about this thread.

Yes, we need a measure of "Condorcetness" or "pairwise bestness". But, like the raw sum-of-utility measure, it doesn't need to be resistant to strategy or motivated by similar concerns that would apply to an actual voting system. It is only motivated by the philosophical "goodness" (representativeness) of the candidate, but I don't know Condorcet systems enough to know what that would be.

@jack-waugh I've always thought Approval ballots should have explicit "Disapprove" boxes alongside the "Approve" boxes, so voters perceive everyone as getting one vote per candidate. (It would also make it harder to tamper with the ballots by adding marks that weren't put there by the voter.)

I've heard of three different ways to count Borda-like ballots

• "each one receives n – 1 points for a first preference, n – 2 for a second, and so on"
• "As Borda proposed the system, each candidate received one more point for each ballot cast than in tournament-style counting, eg. 4-3-2-1 instead of 3-2-1-0"
• Sum up the rankings themselves and elect the candidate with the lowest sum

I've always assumed these are exactly equivalent, and will always elect the same candidate with a given set of ballots, but I want to make sure I'm not missing something. Are they the same even in cases where incomplete rankings are allowed, and in cases where equal rankings are allowed?

Kristofer set up a browseable archive:

https://munsterhjelm.no/km/yahoo_lists_archive/

The forums I've archived have at least one message with at least one of
the terms "center squeeze", "Condorcet", "d'Hondt", "favorite betrayal",
"monotonicity", "Range voting", "Ranked Pairs", Sainte Lague", "Schulze
method" or "Score voting".

The browseable parts have the /web/ foldername:

https://munsterhjelm.no/km/yahoo_lists_archive/sd-2/web/2005-April/by-date.html

https://munsterhjelm.no/km/yahoo_lists_archive/sd-2/web/2005-April/msg00013.html

https://politicalreform.ie/2023/10/06/my-word-preferendum-et-maintenant-le-preferendum/

But there’s another problem: Jean-Charles de Borda’s voting procedure is not exactly the same as that which today is called the Borda Count BC. He suggested that, in any vote on n options, where the voter casts m preferences, points shall be awarded to (1st, 2nd … last) preferences cast, according to the rule

(m, m-1 … 1).

But some of his contemporaries in l’Académie des Sciences changed this to

(n, n-1 … 1).

or

(n-1, n-2 … 0).

If every voter has submitted a full ballot, the social choice and social ranking of any m- or n-rule analysis will remain the same. If, however, some voters have submitted only a partial ballot, the difference between the m- and n-rule outcomes can be huge. In brief, the m rule gives a voter’s (x)th preference 1 point more than her (x+1)th preference, regardless of whether or not she has cast that (x+1)th preference. The n rules, in contrast, give he who casts only one preference an (n-1) advantage over all the other options. So on really contentious topics, the BC may not be much better, if at all, than a plurality vote. The m rule, however, is unbiased. The n-rules promote division, whereas the m-rule can be the very catalyst of consensus; and the m-rule, Jean-Charles’ original proposal, is today known as the Modified Borda Count MBC, a magnificent Irish contribution to the world’s politics.

@toby-pereira said in GPT and I invented a new voting system metric?:

I think if a measure isn't cloneproof it's probably not a good measure.

Why would that matter for a measure?

Also, Copeland is very low resolution anyway in that it just looks at number of defeats rather than the size of any of them.

That makes sense.

From Slack:

Fellow NY'rs, action is needed! SB5259 has been placed on the calendar and would direct the state BOE to study implementing Ranked Choice Voting statewide. It needs to include STAR voting at the minimum if not more options as well. No point in a study that doesn't consider all the solutions to the problem.

Visit NYsenate.gov and Ask your senator & the sponsors (Liz Kreuger & Rachel May) to include STAR voting. We need a comprehensive study if we are going to spend public money on something this important. Feel free to leave a comment (different than sending a message) and vote Aye or Nay on this bill as you see fit (I believe you can change it later if it gets amended, I voted Aye.) You can also go further by tweeting at them if you have a twitter account.
https://www.nysenate.gov/legislation/bills/2023/s5259

In my letter I focused on the motivations mentioned in the bill:

Many advocates argue that ranked choice voting promotes consensus candidates acceptable to the largest number of voters and prevent factional candidates from winning crowded races with less than majority support.

And linked a bunch of research/articles about how the proposed method doesn't actually deliver on this promise. It would be great if a lot of other people could write them and tell them to include better methods in their study, lest we get stuck with Hare RCV.

If your senator is Republican, make sure to mention that neither FPTP nor Hare RCV (would have) worked for them in Alaska, but better consensus-focused voting methods would have won them a seat.

@toby-pereira Sorry I wrote my previous short comment in line at the grocery store and forgot about this thread.

Yes, we need a measure of "Condorcetness" or "pairwise bestness". But, like the raw sum-of-utility measure, it doesn't need to be resistant to strategy or motivated by similar concerns that would apply to an actual voting system. It is only motivated by the philosophical "goodness" (representativeness) of the candidate, but I don't know Condorcet systems enough to know what that would be.

@toby-pereira Criteria and strategy aren't relevant though; it's just a measurement of the "goodness" of the candidate.

@jack-waugh You can also draw parallels to referendums or judge elections where you can vote for or against each item, or abstain.

Me:
What's a good word to fill in the blank?

"Our current voting system suffers from vote-splitting and the spoiler effect, which can cause the election of unrepresentative or extremist candidates that aren't actually the favorite of the voters. A better voting system would always elect the ______ candidate."

Meaning that in a field of candidates with fixed ideological positions, as the voters change their minds and move around the ideological space, the candidate selected by the voting system reflects their ideology as best as possible.

I sometimes say "moderate" or "centrist", by which I mean "relative to the voters' changing ideology", but those words by themselves give the impression that we want to elect a centrist on some absolute scale, even if the voters move away from that position, which is not what we want.

"Most-representative" is the most accurate term, but somewhat awkward. "Consensus candidate" also works pretty well, but is somewhat vague.

What other words would be better to fill in the blank?

ChatGPT:
A suitable word to fill in the blank could be "aligned" or "congruent":

"… A better voting system would always elect the aligned/congruent candidate."

These terms convey the idea that the elected candidate's ideology matches or closely corresponds to the voters' shifting ideologies, without implying an absolute centrist position.

Me:
Got anything else?

ChatGPT:
Certainly, another suitable word to fill in the blank could be "reflective":

"… A better voting system would always elect the reflective candidate."

This term suggests that the elected candidate's ideology mirrors or accurately represents the voters' evolving views, without implying a fixed centrist position.

Me:
I guess that's OK, but it's still going to require a bunch of explanation.

ChatGPT:
I understand your concern. Another option could be "responsive":

"… A better voting system would always elect the responsive candidate."

The term "responsive" conveys that the elected candidate is adaptable and able to adjust their stance in accordance with the shifting ideologies of the voters, without assuming a fixed centrist position. It still may require some explanation, but it should be more intuitive to understand.

Me:
But that's not what I want to convey. The candidate isn't changing their ideology to match the voters. The candidate that wins is changing to a different candidate who better matches the ideology of the voters.

ChatGPT:
Apologies for the confusion. In that case, you might consider using "best-matching" or "ideologically compatible":

"… A better voting system would always elect the best-matching/ideologically compatible candidate."

These terms emphasize that the winning candidate's ideology is the one that best aligns with the voters' views, rather than suggesting the candidate themselves is changing their stance.

Me:
Meh. The best word so far is still "consensus", I think, but that conflicts somewhat with the concept of "consensus decision-making", which is a bit different from a typical voting system.

ChatGPT:
I understand the concern with the term "consensus." In light of that, you might consider using "optimal representative":

"… A better voting system would always elect the optimal representative."

The term "optimal representative" suggests that the elected candidate is the one who best represents the voters' views at any given time, without implying that the candidate themselves is changing their stance or using "consensus" which might cause confusion with consensus decision-making.

@jack-waugh I've always thought Approval ballots should have explicit "Disapprove" boxes alongside the "Approve" boxes, so voters perceive everyone as getting one vote per candidate. (It would also make it harder to tamper with the ballots by adding marks that weren't put there by the voter.)

(Also remember that in the real world, very few people vote honestly under FPTP with more than two candidates, so with party primaries eliminating all but the "two evils", and tactical voting for the "lesser of the two" factored in, it would likely look more like the Top-Two Runoff plot.)

Cooper 2001 makes a good point about SUE vs CE:

while the concept of Condorcet efficiency permits comparison of rules, the dichotomous nature of its evaluation renders it less than perfect. To see why, consider the following example:

A population arrayed along an axis running from −10 to +10, and with a median of 0, chooses between three candidates, located at positions 1, 2, and 8. The candidate at position 1—nearest the median—is of course the Condorcet winner. Decision rule A selects the candidate at position 1 fifty percent of the time and the candidate at position 2 fifty percent of the time. Decision rule B also selects the candidate at position 1 fifty percent of the time, but the remaining fifty percent it chooses the candidate at position 8.

[Condorcet Efficiency] rates decision rules A and B as equivalent, since each selects the Condorcet candidate 50 percent of the time. Yet surely these rules differ in an important way, since rule A selects a candidate near the median—though not that nearest the median—the remaining 50 percent of the time, whereas rule B selects the most extreme candidate the remaining 50 percent of the time.

She then introduces a new metric which "resembles in spirit the concept of social-utility efficiency":

I therefore use a different measure of a decision rule's efficiency. Specifically, I adapt the concept of the Mean Squared Error (MSE) …

Although social utility involves a different calculation (the ratio between the utility of the selected candidate and that of the utility-maximizing candidate), it, like the MSE, involves not merely a ranking of candidates, but a means of capturing the intensity of voters' preferences.

But her "MSE" measurement seems pretty different in concept to me, and is still based on utility, rather than pairwise rankings/defeats like CE is.

Green-Armytage 2015 defines Utilitarian Efficiency to be analogous to CE:

In this paper we define utilitarian efficiency operationally as the likelihood that sincere voting will result in the election of the candidate who maximizes the sum of the voters’ utilities. To the extent that we view elections as a way to select the ‘best’ candidate, utilitarian efficiency is a logical criterion to consider, because maximizing the sum of utilities is a plausible operational definition of being ‘best’.

So, ignoring MSE, the other three metrics can be placed in a table:

So I've been meaning to see if there is an actually analogous metric that fills in the blank. I asked some machines (ChatGPT3.5, Bing Chat, Character.ai) a few week ago if they knew of any, and they did not, so I asked them to complete the analogy, and with some prodding they stumbled around and came up with definitions and some OK names for it.

Then when ChatGPT4 was released, I asked, and it immediately understood what I was asking, invented a metric and name, and wrote out the whole derivation:

Apologies for any confusion. I'm glad to help define this new concept. Here's a possible formula for Pairwise Ranking Efficiency (PRE):

Let's denote the following variables:

• n as the number of candidates
• W as the elected candidate in a given election
• C as the Condorcet winner (assuming one exists)
• p(x, y) as the fraction of pairwise comparisons that candidate x wins against candidate y (0 <= p(x, y) <= 1)

Now, let's define the average pairwise winning fraction for a candidate x:

APWF(x) = (Σ [p(x, y)] for all y ≠ x) / (n - 1)

The Pairwise Ranking Efficiency (PRE) can then be calculated as:

PRE = (APWF(W) - APWF_avg) / (APWF(C) - APWF_avg)

where APWF_avg is the average APWF for all candidates:

APWF_avg = (Σ [APWF(x)] for all x) / n

This formula computes the Pairwise Ranking Efficiency by comparing the performance of the elected candidate (W) with the average candidate performance and normalizing it with respect to the performance of the Condorcet winner (C). The resulting value will range from 0 to 1, where a higher value indicates better performance in electing candidates with strong pairwise ranking properties.

It's not quite right, because:

• "Fraction of pairwise comparisons" (0–1) is not the same units as n-1. Probably the (n-1) should just be dropped, because it's already a fraction? Or just use the count directly, since every term is going to be divided by the same thing anyway?
• There may not always be a Condorcet winner (to be conceptually equivalent, it should compare to the "best" candidate, even if there is no CW)

People who are more familiar with the subtleties of Condorcet systems than me: Does this make sense as a conceptual parallel?

Social Utility Efficiency (=Voter Satisfaction Efficiency) is defined as:

• (Utility(selected) - Utility(average))/(Utility(best) - Utility(average))

So for a ranking-based equivalent, we need to keep the (S-A)/(B-A) concept, but instead base it on number of pairwise defeats? So if CBB(x) = "Number of candidates beat by x", I think this is a simpler equivalent of GPT's idea?:

• (CBB(selected) - CBB(average))/(CBB(best) - CBB(average))

Or do we have to do "number of candidates beaten by x minus number of candidates that beat x" to account for ties? I don't think those are equivalent?