ABC voting and BTR-Score are the single best methods by VSE I've ever seen.
-
@cfrank said:
@ex-dente-leonem can you describe the conditions? For example, what is the generic PVSI without a specified strategy? Is it a mean over a bunch of simulations with agents using random strategies?
As best as I can tell, the generic PVSI examines (from the point of view of the pivotal voter in a faction which changes the outcome) viability-aware strategies for specific voting methods, which in the case of STAR means:
Balance strategic exaggeration (using 5's and 0's instead of 3's and 2's to maximize influence in the scoring round) with the competing incentive of not wanting to give multiple viable candidates the same score. (This yields more 5's and 0's than the naive strategy and is mostly unaffected by the presence of non-viable candidates in the race.)
while the detailed one looks at the effectiveness of targeted strategies by whichever faction would benefit most from those strategies.
I used the same va-ballots and strategies as STAR for BTR/BNR-Score and ABC, partially because of the similar conflict between maximizing support for preferred candidates while taking later rounds into consideration, but mostly to make as few assumptions and to keep conditions as identical as possible.
Also I would like to learn more about agent based modeling and reinforcement learning in this context, I think it could give really interesting results. Finally, how many candidates were there and how were they generated? Probably I’ll have to read the paper.
Each of the 4000 simulated elections is run with 6 candidates and 101 voters (the difference between 101 and 5001 being minimal) on a hierarchical Dirichlet clustered spatial voter model. I'll run some 3-, 9-, and 12-candidate tests later, and I'm very interested in whether the same performance holds up in other simulations and models.
-
@ex-dente-leonem 3x better than what we got so that’s great! Typically how many dimensions are used for candidate platforms in these kinds of simulations?
-
@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
@toby-pereira said:
@ex-dente-leonem Is Viability-aware just strategic voting?
More or less; each simulated election is preceded by an approval poll which factors into viability-aware strategies.
Also how do all the methods do under one-sided strategy? So strategic voting versus honest voting.
The original vse-sim had one-sided strategy analysis, but the newest version appears to have dropped that in favor of Pivotal Voter Strategic Incentive, which seems to measure how much coordination by one faction it takes to change the outcome. The lower the coordination needed, the greater the PVSI, while near-zero means little strategic effect and negative PVSI indicates greater risk of the strategy backfiring.
I see. While also a useful metric, it is different enough for it to be worth having both. As it is we just see the VSE scores and separately this co-ordination measure. But it would be nice to know how much it could drop the VSE by.
-
Ex dente leonem gave these instructions for ABE voting:
Rate each candidate from A to F, A being best and F being worst.
Candidates receive 1 point for each A, B, or C rating and 0 points for each D, E, or F rating.
Equal ratings are allowed. Unrated candidates are automatically rated F.
An explanation for voters:
*The points seed a tournament. The first game matches the candidates with the two lowest point totals.
In each game, the A, B, C, D, E, F ratings determine which candidate is preferred by each voter. If you gave candidate Mike a D, and candidate Tim a B, your vote would go to Tim.
The winner would face the candidate with the next lowest number of points. This is repeated until the survivor meets the candidate with the highest number of points in the final game to determine the winner.
A spoiler effect is nearly impossible with ABC voting.*
ABC is one notch more complex than BTR-Score, which is quite simple as Condorcet methods go.
Is “nearly impossible” a fair statement?
What other benefits should we highlight for the public?
Were you using Jonathan Quinn’s VSE?
Thanks for the great thread.
-
I have to admit that I'm confused by the results. I did expect BTR-score to perform well, but I also thought that the difference to Smith//score would be to small to measure. I wonder why there is such a big difference.
Also, when looking at viability-aware, STAR performs a lot better, which is also surprising. Is it that it better utilizes the score part and therefor gets the "best of both worlds"? I don't know.
How long does it take for you to run those simulations?
If it's not too much work, could you try out MARS? It's basically like BTR-score, but each round does not only compare votes, but votes+scores (both measured in % of maximum possible). Previously I thought that that would be even better than BTR-score (on the cost of being complicated), but now I'm no longer sure.
One thing to be cautious of is that these results present very small differences in a high range. It might be that the choice of model has too much of an influence to make decisive claims.
ABC is a good idea and I think could be really a viable method when fleshed out. Most importantly I think there may be more intuitive ways to preset it. Maybe something in between scores and approval, like "ABC-123" where letter ratings count as 0 and numbers as scores.
-
@cfrank Apologies for the late response; most of the voter model is a black box to me but this from the earlier version (in reference to a less complex model):
Voters and candidates each have a location in n-dimensional “ideology space”. A voter’s satisfaction for a given candidate goes down linearly with the ideological distance between the two. Locations are normally distributed, using the same distribution for candidates and voters; and the standard deviations for each dimension follow an exponentially descending sequence such as 1, 1/2, 1/4, 1/8, etc. The number of dimensions is set so as to be large enough that further dimensions would be insignificant. Thus, the only important parameter is the rate of exponential decay; in the example sequence above, it’s 2.
implies it's quite a large number.
-
@toby-pereira I'd like to see that as well. I'll take some time to check out the original CES vse-sim and compare results on both.
-
@gregw said:
A spoiler effect is nearly impossible with ABC voting.*
Is “nearly impossible” a fair statement?
That seems fair, as it requires a cycle of at least four candidates in a specific configuration.
What other benefits should we highlight for the public?
Voters disinclined to vote for the lesser of two evils but also seeking to mitigate their worst outcome can safely do so without actually supporting the less disfavored of two unpopular frontrunners, as expressing preference in ABC doesn't necessitate support, and their full votes can go to more preferred alternatives. I also like that the mechanic is evocative of letter grading and allows voters to rate candidates in a sense similar to what we're already familiar with.
Were you using Jonathan Quinn’s VSE?
Yes, it can be found here.
Thanks for the great thread.
Much appreciated, thank you.
-
@casimir said:
I have to admit that I'm confused by the results. I did expect BTR-score to perform well, but I also thought that the difference to Smith//score would be to small to measure. I wonder why there is such a big difference.
I was wondering the same actually, and I think it may have something to do with how strategic voting is evaluated with Smith methods in vse-sim, specifically existing base methods run on Smith sets. For one thing the only targeted strategy available for analysis by default is bullet voting. I suggest disregarding PVSI and va behavior for Smith//Score and just looking at honest voters, which seem in line with expectations.
Also, when looking at viability-aware, STAR performs a lot better, which is also surprising. Is it that it better utilizes the score part and therefor gets the "best of both worlds"? I don't know.
My speculation is that STAR's single runoff as compared to BTR-Score's several widens the window of advantage for strategy.
How long does it take for you to run those simulations?
It depends on how many moving parts there are, but to give a rough idea here's how many minutes it takes to run 200 elections with 101 voters and 6 candidates on the following methods:
STAR - 1:38
BTR-Score: 1:49
BNR-Score - 2:51
ABC - 1:58
MARS - 1:54 (This one was a pleasant surprise)But should be a lot faster on newer machines.
One thing to be cautious of is that these results present very small differences in a high range. It might be that the choice of model has too much of an influence to make decisive claims.
Very true, but given that these replicate as closely as possible the conditions of the STAR paper (which is cited as part of official advocacy efforts), I believe they're definitely worthy of attention. That said, these are all excellent methods VSE-wise, and I think most importantly underline how powerful sequential pairwise elimination is as part of any hybrid method,.
If it's not too much work, could you try out MARS? It's basically like BTR-score, but each round does not only compare votes, but votes+scores (both measured in % of maximum possible). Previously I thought that that would be even better than BTR-score (on the cost of being complicated), but now I'm no longer sure.
 Have I got great news for you... The title of this thread is officially obsolete.
Have I got great news for you... The title of this thread is officially obsolete.Here are the result of 4,000 elections:
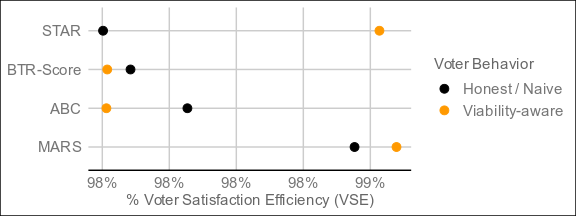
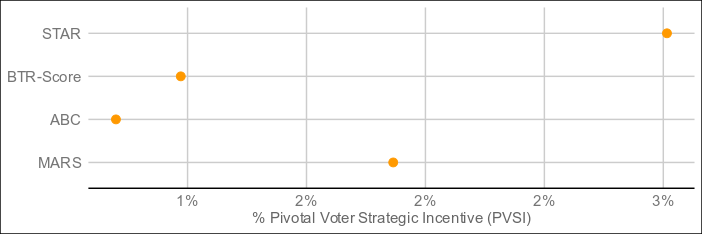
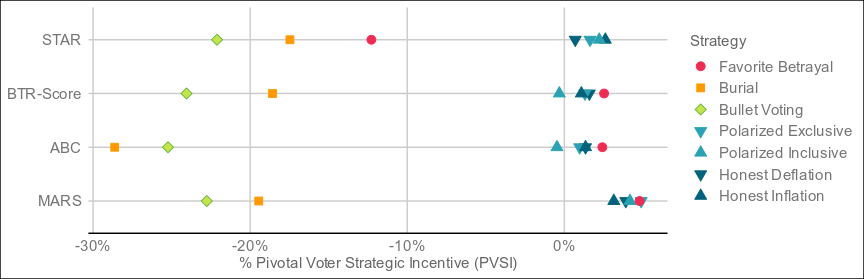
The undisputed best performer by VSE of the four is MARS, which threads the needle between Condorcet and utility methods by being neither and both, and blazing ahead as a result. The resolution mechanism is a step more complex than bottom-two runoff, but still less so than a full pairwise preference matrix (with potentially better results than such), and it resolves in around the same time as ABC and BTR-Score. For electorates who don't care too much about what's under the hood as long as it's transparent, this might be the one.
-
Thanks for these simulations, they're definitely interesting @Ex-dente-leonem

That said, I think we might be making the mistake of getting sucked deeper and deeper into a drunkard's search. The simulation results here don't really say much, except that we haven't figured out a strategy that breaks Smith//Score or ABC voting yet. That's not surprising, given we only tested 5 of them.
The difficult part of modeling voters isn't showing that one strategy or another doesn't lead to bad results. It's showing that the best possible strategy leads to good results. There's nothing wrong with testing out some strategies like in these simulations, but these are all preliminary findings and can only rule voting methods out, not in.
Just because every integer between 1 and 340 satisfies your conjecture, doesn't mean your conjecture is true. You still need to prove your conjecture.
This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.
The methodology here completely fails to pick up on this, because it only tests pure strategies (i.e. no randomness and everyone plays the same strategy). In practice, pure strategies are rarely, if ever, the best. Ignoring mixed strategies has led the whole field of political science on a 15-year wild goose-chicken-chase that would've been avoided if anyone had taken Game Theory 101.
-
@lime said:
The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.
I don't believe Ranked Pairs is analyzed in the STAR paper, unless you're thinking of Jameson Quinn's original VSE document or a different paper.
I think the important takeaway here is less about trying to game out every strategy possible than the fact of how these models perform under the same conditions as what the authors believe to be their best modeled simulations, given that such simulations are an integral part of EVC's and others' advocacy efforts. (For quite necessary reasons, as we have no historical results for many methods, and as noted such historical samples would likely be unacceptably small or fail to capture the development of strategy over time.) I'd definitely welcome further testing in other simulations with mixed strategies and other voter models as realistic as we can make them.
I believe the above should be taken as impetus for theoretical analysis of why these methods seem to perform so well, and the key may be that they're all hybrid methods involving pairwise comparisons and sequential eliminations for all candidates at some point, which reasonably makes potential strategies that much harder to coordinate.
-
@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
 Have I got great news for you...
Have I got great news for you...Thank you very much. That's even better than I expected.
-
@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.
I believe you are referring to this chart? Which shows Ranked pairs and Schulze as doing slightly better than STAR with honest voting. Does Schulze also have some failure mode which makes honest voting not the game theoretical optimal vote?
-
@ex-dente-leonem said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
@lime said:
The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.
I don't believe Ranked Pairs is analyzed in the STAR paper, unless you're thinking of Jameson Quinn's original VSE document or a different paper.
I think the important takeaway here is less about trying to game out every strategy possible than the fact of how these models perform under the same conditions as what the authors believe to be their best modeled simulations, given that such simulations are an integral part of EVC's and others' advocacy efforts. (For quite necessary reasons, as we have no historical results for many methods, and as noted such historical samples would likely be unacceptably small or fail to capture the development of strategy over time.) I'd definitely welcome further testing in other simulations with mixed strategies and other voter models as realistic as we can make them.
I believe the above should be taken as impetus for theoretical analysis of why these methods seem to perform so well, and the key may be that they're all hybrid methods involving pairwise comparisons and sequential eliminations for all candidates at some point, which reasonably makes potential strategies that much harder to coordinate.
I'm talking about the original VSE document, yes. And my point is that I think the strategic voting assumptions are wholly unrealistic to the point that they will probably miss the vast majority of pathologies, like it does for Ranked Pairs and Schulze.
-
If we're going to put candidates into a tier list, we ought to include an S tier worth >1 point. I am curious about what effect that would have. Is the code used to run the ABC simulations open source?
-
@k98kurz said:
If we're going to put candidates into a tier list, we ought to include an S tier worth >1 point. I am curious about what effect that would have.
Infinite meme potential
Is the code used to run the ABC simulations open source?
Sure, here's Jameson Quinn's vse-sim and the relevant code is:
def makeLexScaleMethod(topRank=10, steepness=1, threshold=0.5, asClass=False): class LexScale0to(Method): """ Lexical scale voting, 0-10. """ bias5 = 2.3536762480634343 compLevels = [1,2] diehardLevels = [1,2, 4] @classmethod def candScore(cls,scores): """ Takes the list of votes for a candidate; Applies sigmoid function; Returns the candidate's score normalized to [0,1]. """ scores = [1/(1+((score/cls.topRank)**(log(2, cls.threshold))-1)**cls.steepness) if score != 0 else 0 for score in scores] return mean(scores) """ """ LexScale0to.topRank = topRank LexScale0to.steepness = steepness LexScale0to.threshold = threshold if asClass: return LexScale0to return LexScale0to() class LexScale(makeLexScaleMethod(5, exp(3), 0.5, True)): """ Lexical scale voting: approval voting but retains preferences among both approved and disapproved options. """ passto convert Score to 'Lexical Scale', and then to change STAR-style automatic runoff to sequential pairwise elimination:
def makeABCMethod(topRank=5, steepness=exp(3), threshold=0.5): "ABC Voting" LexScale0to = makeLexScaleMethod(topRank, steepness, threshold, True) class ABC0to(LexScale0to): stratTargetFor = Method.stratTarget3 diehardLevels = [1,2,3,4] compLevels = [1,2,3] @classmethod def results(cls, ballots, **kwargs): baseResults = super(ABC0to, cls).results(ballots, **kwargs) candidateIndices = list(range(len(baseResults))) remainingCandidates = candidateIndices[:] while len(remainingCandidates) > 1: (secondLowest, lowest) = sorted(remainingCandidates, key=lambda i: baseResults[i])[:2] upset = sum(sign(ballot[lowest] - ballot[secondLowest]) for ballot in ballots) if upset > 0: remainingCandidates.remove(secondLowest) else: remainingCandidates.remove(lowest) winner = remainingCandidates[0] top = sorted(range(len(baseResults)), key=lambda i: baseResults[i])[-1] if winner != top: baseResults[winner] = baseResults[top] + 0.01 return baseResults """ """ if topRank==5: ABC0to.__name__ = "ABC" else: ABC0to.__name__ = "ABC" + str(topRank) return ABC0to class ABC(makeABCMethod(5)): passAny suggestions for improvement or optimization greatly welcome.
-
@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
Thanks for these simulations, they're definitely interesting @Ex-dente-leonem

That said, I think we might be making the mistake of getting sucked deeper and deeper into a drunkard's search. The simulation results here don't really say much, except that we haven't figured out a strategy that breaks Smith//Score or ABC voting yet. That's not surprising, given we only tested 5 of them.
The difficult part of modeling voters isn't showing that one strategy or another doesn't lead to bad results. It's showing that the best possible strategy leads to good results. There's nothing wrong with testing out some strategies like in these simulations, but these are all preliminary findings and can only rule voting methods out, not in.
Just because every integer between 1 and 340 satisfies your conjecture, doesn't mean your conjecture is true. You still need to prove your conjecture.
This isn't just hypothetical. The CPE paper shows very strong results for Ranked Pairs under strategic voting. This is well-known to be wildly incorrect: the optimal strategy for any case with 3 major candidates is a mixed/randomized burial strategy that ends up producing the same result as Borda, i.e. the winner is completely random and even minor (universally-despised) candidates have a high probability of winning.
The methodology here completely fails to pick up on this, because it only tests pure strategies (i.e. no randomness and everyone plays the same strategy). In practice, pure strategies are rarely, if ever, the best. Ignoring mixed strategies has led the whole field of political science on a 15-year wild goose-chicken-chase that would've been avoided if anyone had taken Game Theory 101.
What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters. Not under the assumption that a particular simplistic strategy model gives good results, and not even that the game theoretically optimal strategy leads to good results, but that real life voter behaviour would lead to good results.
-
@toby-pereira said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters.
To test any system in real elections we need to make the claim that the “new” system is better than the current system.
That is not a high bar, as the current system is plurality voting. IRV is also a competitor.
We may not have a firm handle on how good ABC or BTR-Score are, but we can say they are better than the choices above.
-
@toby-pereira said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
What we really need (and which is unattainable right now for most methods) is to see what would happen in real life elections with real voters. Not under the assumption that a particular simplistic strategy model gives good results, and not even that the game theoretically optimal strategy leads to good results, but that real life voter behaviour would lead to good results.
Technically yes, but I'd feel very uncomfortable with any method where the game-theoretically optimal strategy leads to bad results, even if experiments showed the method doing well. I'd be worried voters just haven't figured out the correct strategy yet, and as soon as someone explains it to them all hell will break loose.
This is how Italy's parliament got so screwed up. They had a theoretically proportional mechanism that can be broken. It looked fine at first—because it took Berlusconi 2 or 3 election cycles to recognize the loophole and exploit the hell out of it.
So, in other words, you need an actual proof, not just "well, when I tried a couple strategies..." Otherwise, you'll find out 5-10 years later that there's some edge case where your method is a complete disaster, and after the whole IRV fiasco, electoral reform will end up completely and thoroughly discredited. (Italy went back to a mixed FPP-proportional system after the screwup.)
-
@lime said in ABC voting and BTR-Score are the single best methods by VSE I've ever seen.:
I'd feel very uncomfortable with any method where the game-theoretically optimal strategy leads to bad results, even if experiments showed the method doing well. I'd be worried voters just haven't figured out the correct strategy yet, and as soon as someone explains it to them all hell will break loose.
Are you uncomfortable with BTR-Score? As a Condorcet method, it should be safer than most new systems. It would elect the “beats all” winner if there is one. Otherwise, it would elect someone from the Smith set.
As with any cardinal system, one side could decide to always bullet vote giving their favorite the highest rating and everybody else 0. The punishment would be harm to their second choices.
Would this be more, or less of a problem with BTR-Score?
Do you see another possible weakness? If so, how bad?
BTW VotersTakeCharge.us is under construction.
For a sneak peek, use the following login:
user: flywheel
Pass: squalid-fiction