Citing Copeland vs. Citing Llull
-
We associate with Copeland the method of electing the candidate who beats the most count of other candidates, where "beats" means receives more preferences over that candidate than the other candidate receives over the given candidate. Llull invented almost the same method much earlier than Copeland. However, even in the version Llull described that is closest to Copeland's, the treatment of candidates receiving equal numbers of preferences differs from Copeland's. So, it makes sense to cite Copeland if we mean his exact method.
-
@jack-waugh And Condorcet himself described this method before Copeland. It always seemed to me the most obvious Condorcet method, "count the pairwise ties".
I'll admit to being a bit confused if there can be a Copeland winner (candidate that beats more candidates than anyone else) that isn't a Condorcet winner.
Personally I am more interested in the concept of a Copeland set (all candidates that tie for pairwise winner) and the Copeland score (the number of pairwise wins a candidate has) than any actual method.
-
@rob said in Citing Copeland vs. Citing Llull:
I'll admit to being a bit confused if there can be a Copeland winner (candidate that beats more candidates than anyone else) that isn't a Condorcet winner.
https://electowiki.org/wiki/Ranked_Robin#Tabulation purports to show an example. "Ava pairwise beats the greatest number of candidates, 3, so she is elected as the winner." But to be a Condorcet winner, she would have to beat four other candidates (she doesn't beat Bianca).
-
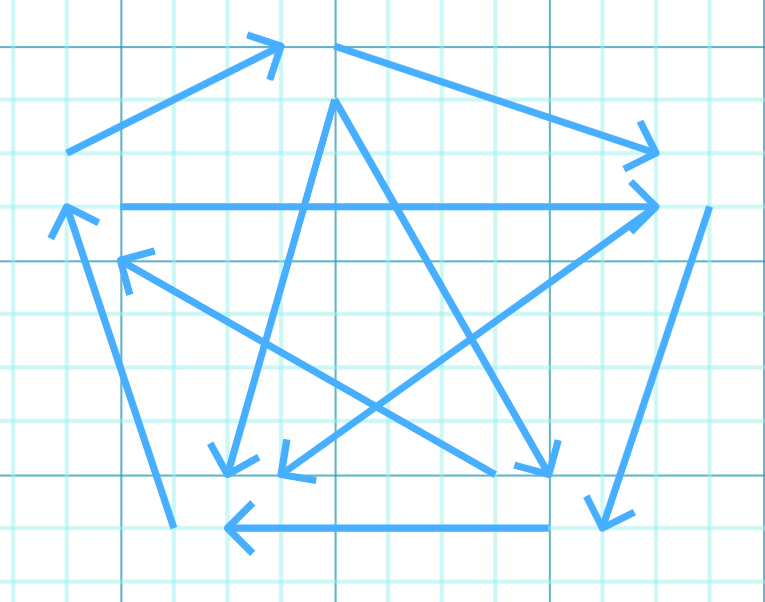
This is what the majority graph looks like for a Copeland winner who is not a Condorcet winner.
Remember that the Copeland set is a subset of the Smith set, so the reverse is impossible (i.e. if there is a Condorcet winner then that is also necessarily the Copeland winner)
A Copeland winner not being a Condorcet winner requires a 5-cycle, so we may as well assume it will literally never happen even once in any real-life election.
-
@andy-dienes Thanks Andy, that's interesting. To be clear, if there is a Condorcet winner, that will always be the Copeland winner, right?
It's just possible, in an extremely rare case, for there to be a Copeland winner when there is no Condorcet winner. Such as a 5 candidate race where the winner only beats 3 other candidates... but the other candidates beat less than 3.
-
@rob yup, both those statements are correct!