What level of PR do different systems get?
-
I think this is a question which does not get talked about enough. The obvious reason is that there are many definitions of PR and no single definition applies to all systems. However..... there is a somewhat meta concept of PR which one can apply across systems since I would not say they are really in conflict. No system can have no PR at all but partisan PR systems can arguably have full PR. I made this plot to try to get the conversation rolling.
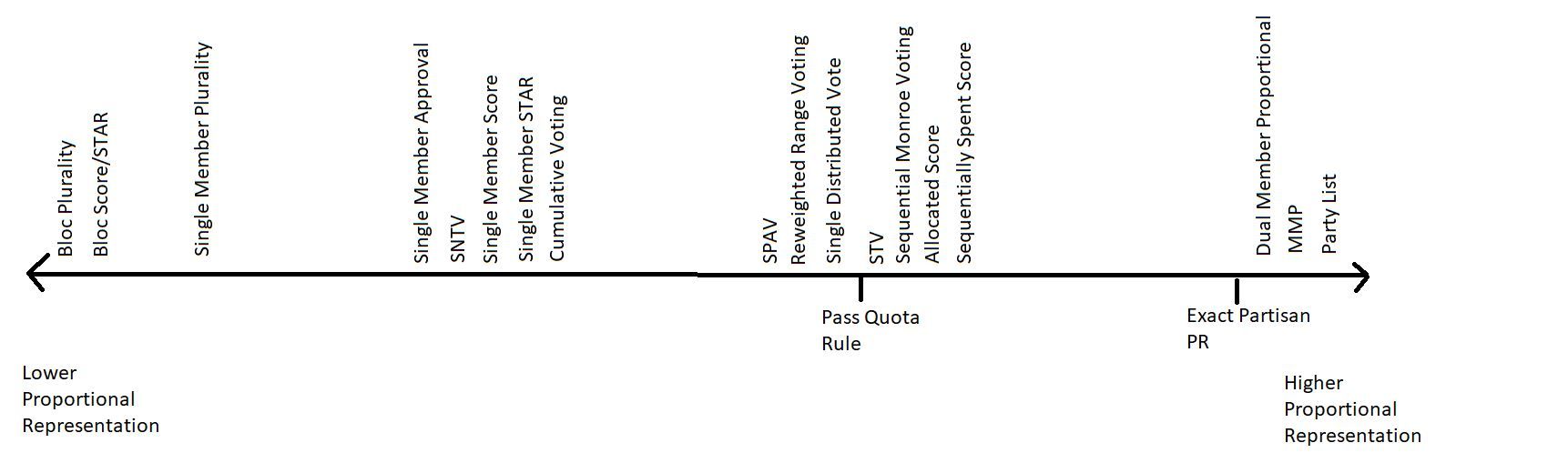
Disclaimers:
- This is likely not to scale though I did my best
- All multimember systems are 5 member
- I put the two touchpoints of passing a quota rule and exact partisan PR. If there were more I would add them
- The sequence of the multimember systems around the quota rule point is based on the Winner set stability definition of PR. Other definitions will give different sequences. For example I think SPAV is the only system of them which passes Proportional Justified Representation but that is not super commonly used since STV fails it.
- These are just the systems which came to mind. I am likely missing a few important ones.
-
Without knowing Keith had made the chart above, I also made a chart to try and hone in on this concept.
That said, I think graphing systems on a chart like this will always get pushback unless it's made with real data, and even then I doubt it's worth sharing...
In any case, single winner elections which elect plurality winners will always have lower PR than those which ensure at least majority support, and methods which take into account voters secondary and tertiary preferences and level of support for other methods will also have a higher level of PR.
Can anyone think of some better multi-winner methods that would qualify as semi-proportional?
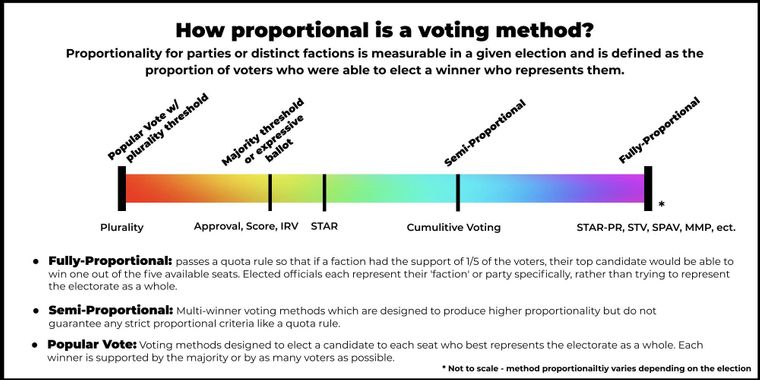
It's worth noting that an electoral system with no PR is possible (dictatorship) and perfect proportionality is also possible if a given election had everyone neatly assigned to a viable sized team, but I focused my chart on the actionable and democratic section of the spectrum.
-
I don't know that partisan PR is more PR than non-partisan PR. It's just less clear what exactly is getting portioned out.
-
@SaraWolk said in What level of PR do different systems get?:
multi-winner methods that would qualify as semi-proportional?
What do you mean by "better"? What about SNTV?
@SaraWolk said in What level of PR do different systems get?:
I don't know that partisan PR is more PR than non-partisan PR. It's just less clear what exactly is getting portioned out.
If everybody votes along party lines then partisan systems are have higher PR than 5 winner systems because they elect the whole parliament at once instead of just 5. The resolution of a system is the number of winners in a riding. Although, many such systems put in limits of needing 5%.
@SaraWolk said in What level of PR do different systems get?:
It's worth noting that an electoral system with no PR is possible (dictatorship)
Well sort of. That dictator will a least represent themselves so there is a tiny amount of PR.
It would be interesting to try to simulate this. We would have to make a bunch of assumptions and choose a way to map candidate endorsement to party endorsement in a realistic way. But if we did have such a simulation we could then calculate an average Gallagher index for each system.
@SaraWolk I am surprised you put Single Member STAR so far from Cumulative voting. I would think they would be much closer. But without a simulation I only have intuition to go on.
-
@Keith
For "better" semi-proportional methods for inclusion in a chart I mean methods in use or that people are familiar with. Or methods that are too fabulous to not include. What's SNTV?Re Party List vs. nonpartisan PR, the difference there is the number of winners, not the partisanship.
I have no idea where exactly STAR or Cumulative should go, or which order they would go in. I'd like to think they should be reversed, but I also have no basis for that.
-
@SaraWolk said in What level of PR do different systems get?:
What's SNTV?
https://electowiki.org/wiki/Single_non-transferable_vote
@SaraWolk said in What level of PR do different systems get?:
Re Party List vs. nonpartisan PR, the difference there is the number of winners, not the partisanship.
Granted but if you partisan vote then the same ballot works for any number of winners. Parliaments are typically over 100 seats. You are never going to run a ballot with candidates for so many seats. So what I am saying is true in practice but not necessarily in theory.
@SaraWolk said in What level of PR do different systems get?:
I have no idea where exactly STAR or Cumulative should go, or which order they would go in. I'd like to think they should be reversed, but I also have no basis for that.
I do not have the time to write simulation code. If only there were universities who would sponsor people to study this.
-
Disproportionality can be divided into two components:
-
Random fluctuations from exact proportionality
-
Bias (by size).
STV & Largest-Remainder have unnecessarily high #1.
Other than that, the divisor (highest average) methods differ unimportantly in #1.
#1 is relatively unimportant because it’s just a tiny (for divisor methods) fluctuation bringing no unfairness.
#2, bias, is what matters.
Sainte-Lague is the allocation rule with virtually zero bias.
It’s bias is very, very nearly zero. …a very, very tiny bias toward the large.
Is you want absolutely zero bias, then use Biad-Free.
Where Sainte-Lague rounds off to the nearest integer, with (a+b)/2, = a + .5 as its rounding point, Bias-Free’s rounding point is determined as follows:
Divide b^b by a^a. Then divide the result by e.
…where e is the base of natural logarithms, = about 2.718…
That rounding point is called an “identical-mean
-
-
Bias-Free’s rounding point is called an “Identric-mean. Autocorrect changed “ identric” to “identical”.
That mean has been much discussed in mathematics, but, according to a journal-paper, my EM post was the first proposal to use it for the unbiased divisor-method rounding point.
-
@michaelossipoff I want to return to this "bias-free" method actually.
We briefly had a discussion on EM. Here is my post and here is your reply.
But in summary: I argued that Sainte-Laguë is actually unbiased, whereas you argued that it is slightly biased towards large parties. However, I'm not sure you fully got the point I was making, and I think we are perhaps using different definitions of bias.
As I understand it, your "bias-free" method works to ensure that neither small nor large parties are over-represented as a whole.
Whereas my argument is that Sainte-Laguë still gives objectively the most proportional result. However, due to the statistical make-up of party votes under certain assumptions, large parties as a whole may still be over-represented.
My argument is also that large parties do not form a coalition and neither do small parties, so a bias towards one or the other because of statistical voting patterns should not be countered. I'll use my previous examples:
4 to elect:
A: 38
B: 38
C : 12
D : 12Under Sainte-Laguë, A and B get two seats each. One might see this as a large-party bias and say that a more balanced result is to take a seat from one of the large parties and give it to a small party. And the other example:
A: 37
B: 37
C : 13
D : 13In this example under Sainte-Laguë, all four parties get one seat each. One might see this as a small-party bias and argue that a more balanced result would be to take a seat from one of the small parties and give it to a large party.
However, the problem with the reasoning in both these cases is that the parties are not in coalition. In the first example, the votes were just over the threshold so that the large parties won all the seats. They are both over-represented, yes, but giving a seat to a small party would also be over-representation. The two large parties have nothing to do with each other, so talking of a large-party bias is not the right way to look at it. However it is done, two parties will be over-represented. Whether they are both large, both small or one of each is beside the point.
-
@toby-pereira said
[quote]
But in summary: I argued that Sainte-Laguë is actually unbiased, whereas you argued that it is slightly biased towards large parties. However, I'm not sure you fully got the point I was making, and I think we are perhaps using different definitions of bias.
[/quote]
Here’s what I mean by bias:
The divisor methods divide each party’s votes by the same number, also called the quota.
The 1st quota used is the Hare quota.
So, divide to determine how many quotas each party has.
Then round off each party’s quotas to the nearest integer, for that party’s seat-allocation.
By trial & error or systematic-procedure, find the quota that results in the desired house-size.
Of course if a party has between a quotas & b quota, then its allocation by that quota rounds to a or b.
So, a & b are any two consecutive integers representing whole numbers of quotas.
The region between a & b, I’ll refer to as an “ interval”. Of course each interval has a width, (a-b), of 1.
All this in order to define “interval.
So here’s what I mean by unbias:
Suppose two parties’ quota-amounts are in two very distantly-separated intervals.
e.g. Say one party’s quotas is in the 0 to 1 interval & the other party’s quotas is in the 100 to 101 interval.
The allocation-rule is unbiased if, in every interval, the average seats per quota (including the fractional part of a quota), averaged over all possible non-integer numbers of quotas in that interval, is the same for all intervals.
e.g. including the 0 to 1 interval & the 100 to 101 interval.
Sainte-Lague, roundly to to the nearest integer, has a + .5, = (a+b)/2, as it’s rounding point.. the arithmetical mean.
Bias Fred’s rounding-point is an “identric mean”, determining as follows:
Divide a^a by b^b. Then divide the result by e.
…where e is the base of the natural logarithms, = about 2.718…
Bias-free is unbiased as I defined that term. With Sainte-Lague, the average seats per vote in a higher interval is slightly greater than that average in a lower interval.
That’s bias vs unbias.
There’s always some random fluctuation from exact proportionality. That isn’t bias. The slight random fluctuation from exact proportionality, universally present in all methods, isn’t problematic or objectionable like the CONSISTSNT & SYSTEMATIC unequal treatment by a biased allocation-rule.
Now, just speaking of minimization of that random departure from proportionality, yes Sainte-Lague (Webster) & “Equal-Proportions” (Huntington-Hill) both have claim of minimizing that (harmless & slight) fluctuation.
SL minimizes it I’m terms of difference between 2 parties’ seats/votes numbers…while Huntington-Hill minimizes it in terms of ratio
of those numbers.To me, of those two, ratio seems more appropriate & meaningful, because s/v is itself a ratio.
Additionally, Huntington gave other good reasons why ratio seems more meaningful.
…& all that is irrelevant, because that slight random fluctuation is harmless & unimportant in comparison to bias, a consistent & systematic disfavoring of small or large parties.
As I understand it, your "bias-free" method works to ensure that neither small nor large parties are over-represented as a whole.
Whereas my argument is that Sainte-Laguë still gives objectively the most proportional result. However, due to the statistical make-up of party votes under certain assumptions, large parties as a whole may still be over-represented.
My argument is also that large parties do not form a coalition and neither do small parties, so a bias towards one or the other because of statistical voting patterns should not be countered. I'll use my previous examples:
4 to elect:
A: 38
B: 38
C : 12
D : 12Under Sainte-Laguë, A and B get two seats each. One might see this as a large-party bias and say that a more balanced result is to take a seat from one of the large parties and give it to a small party. And the other example:
A: 37
B: 37
C : 13
D : 13In this example under Sainte-Laguë, all four parties get one seat each. One might see this as a small-party bias and argue that a more balanced result would be to take a seat from one of the small parties and give it to a large party.
However, the problem with the reasoning in both these cases is that the parties are not in coalition. In the first example, the votes were just over the threshold so that the large parties won all the seats. They are both over-represented, yes, but giving a seat to a small party would also be over-representation. The two large parties have nothing to do with each other, so talking of a large-party bias is not the right way to look at it. However it is done, two parties will be over-represented. Whether they are both large, both small or one of each is beside the point.
-
I emphasize that SL is so nearly unbiased, & its rounding to the nearest integer is so natural & obvious, that SL is an excellent choice, & the best proposal..,unless absolute unbias is desired.
Huntington-Hill is how we apportion the House of Representatives here. …chosen of course because it favors small states.
Huntington-Hill is twice as biased as SL, in the opposite direction.
The Greens. I’m told, use Huntington-Hill to elect their deliberative-body. SL would be only half as biased.
-
-
@michaelossipoff OK, I'll take it on trust for now that your method has the properties you say. However, there are of course different potential measures of bias.
For example, we can see the amount of representation a voter gets as the number of candidates elected from the party they vote for divided by the number of voters of that party. Sainte-Laguë uniquely minimises the variation of this representation, so can be seen as the most accurate proportional party-list method, or indeed, unbiased. Moving the divisors in the D'Hondt direction creates a large-party bias, whereas moving in the other direction creates a small-party bias.
-
@toby-pereira said in What level of PR do different systems get?:
@michaelossipoff OK, I'll take it on trust for now that your method has the properties you say. However, there are of course different potential measures of bias.
[\quote]The alternative definitions aren’t bias.
e.g. see below:
[quote]
For example, we can see the amount of representation a voter gets as the number of candidates elected from the party they vote for divided by the number of voters of that party.
[\quote]Of course seats per vote (s/v) is what should be equal, & that’s what this is all about.
With Sainte-Lague the average s/v, averaged over a higher interval (like 100 to 101) is greater than the average over a lower interval ( like 0 to 1).
[quote]
Sainte-Laguë uniquely minimises the variation of this representation
[/quote]No. That random departure from proportionality, that RANDOM variation of s/v, isn’t bias.
Bias is defined as SYSTEMATIC CONSISTENT favoring of one thing or set (party or set of parties) over another. The random s/v fluctuation itself isn’t bias, by any definition.
SL favors large parties over small ones. That’s bias, by any definition.
As I said, fluctuation of the parties’ s/v is inevitable. If it’s random, if it doesn’t consistently systematically favor on set over another (e.g. large parties over small parties, then it’s not bias.
As I said, that fluctuation is inevitable, & it’s completely unimportant compared to a SYSTEMATIC CONSISTENT disfavoring is small parties.
As I said, both SL & Huntington-Hill (HH) can claim to minimize the fluctuation (while consistently giving larger or smaller parties lower s/v).
SL minimizes the fluctuation in terms of difference in s/v. HH minimizes the fluctuation in terms of ratio of s/v.
But both are biased. SL gives higher s/v to large parties. HH give higher s/v to small parties.
Bias-Free (BF) is completely, absolutely unbiased. It doesn’t favor either larger or smaller
parties.But, as I said:
SL is only half as biased ad HH.
SL’s bias is so tiny, so negligibly tiny, that it’s effectively unbiased. …unbiased for all practical purposes.
e.g. :
150 seats.
17 small parties, each with 3% of the vote.
…totalling 51% of the vote.
One big party with 49% of the vote.
The small parties together get a majority of the seats, & can form a majority coalition & government.
…& of course SL, with its rounding point of (a+b)/2, = a + .5, is the natural obvious intuitive
divisor-method. -
@michaelossipoff I'm not talking about random fluctuation. I'm talking about Sainte-Laguë being the unique method that minimises the representation variance. For any given election the result from "Bias Free" will have an equal to or greater variation than Sainte-Laguë. So before we get to bias, I would say that Sainte-Laguë is objectively more proportional. So for "Bias Free" to indeed be less biased, we'd be saying that proportionality and bias can be varied independently, to some extent at least.
But as for bias, take the following example with 2 to elect:
Party A: 75
Party B: 25Sainte-Laguë gives a tie between 2-0 (both to party A) and 1-1. "Bias Free" systematically favours smaller parties in such a tie case, awarding the parties 1 seat each. This is, as I would see it, bias.
The point is that in any given election, Sainte-Laguë minimises the variation and gives the most proportional result. It might still be that if you look at a large number of elections, large parties fare better on average, but this does rely on certain assumptions about the voting distribution, as I've said previously, rather than being intrinsic to the method. Plus one large party being favoured doesn't mean this should be balanced elsewhere as the large parties are separate entities and not in coalition with each other.
-
@toby-pereira said in What level of PR do different systems get?:
@michaelossipoff
[quote]
I'm not talking about random fluctuation.
[\quote]Talk about it or not, but, with BF, the fluctuation is random only. No bias.
[quote]
I'm talking about Sainte-Laguë being the unique method that minimises the representation variance.
[\quote]Fine, then you aren’t talking about bias.
I explained the difference.
…&, as I also explained 2 or 3 times, SL & HH both have their claim to minimizing that variation.
I pointed out that HH’s measure based on ratio makes more sense because s/v is, itself, a ratio.
Huntington pointed out that the ratio measure of the distance between two s/v values is consistent with a lot of measures, & is therefore less arbitrary. For his argument, I’ll have to refer you to Huntington’s article.
Google “Huntington, Huntington-Hill vs Webster.”
[quote]
For any given election the result from "Bias Free" will have an equal to or greater variation than Sainte-Laguë.
[/quote]…at least by SL’s more questionable (compared to HH) measure of distance between s/v values.
In any case, you’re still confusing bias with variation, something that I’ve explained several times.
[quote]
So before we get to bias, I would say that Sainte-Laguë is objectively more proportional.
[/quote]Less s/v variation by SL’s more questionable difference measure of distance between two s/v values. But as you agreed above, that isn’t bias, & isn’t relevant to the matter of bias.
So for "Bias Free" to indeed be less biased, we'd be saying that proportionality and bias can be varied independently, to some extent at least.
I’ve been trying to explain to you that they’re different topics.
[quote]
But as for bias, take the following example with 2 to elect:
Party A: 75
Party B: 25Sainte-Laguë gives a tie between 2-0 (both to party A) and 1-1.
[\quote]SL doesn’t give an answer, in your special & atypical example.
BF gives each party one seat.
[quote]
"Bias Free" systematically favours smaller parties in such a tie case…
[\quote]Incorrect. One example isn’t a basis for saying “systematically”. “Systematically” refers to something that happens consistently in many
instances.So no, BF doesn’t allocate biasedly in that example.
What is it about that result in that example that makes you think it’s biased?
By the definition of bias, it’s meaningless to say that a single result in a single example is “biased”. I’ve been trying to explain to you what bias means, but evidently I haven’t been getting through.
Bias means what I said. BF is entirely unbiased for the reason that I said. SL is biased in favor of large parties for the reason that I said.
[quote]
…awarding the parties 1 seat each. This is, as I would see it, bias.
[/quote]How so? See above.
[quote]
The point is that in any given election, Sainte-Laguë minimises the variation…
[/quote]Only by its questionable measure of distance between two s/v values.
[quote]*
It might still be that if you look at a large number of elections, large parties fare better on average, but this does rely on certain assumptions about the voting distribution, as I've said previously, rather than being intrinsic to the method.
[\quote]What assumptions? I averaged over all the values that a party’s number of quotas could have in a particular interval.
[quote]
Plus one large party being favoured doesn't mean this should be balanced elsewhere as the large parties are separate entities and not in coalition with each other.
[\quote]Not sure what you mean by that. I told you what bias means.
In your special & atypical example, as I said, SL doesn’t have a result. BF & HH give each party one seat.
In actual SL elections, the 1st rounding-point, in most implementations without a higher threshold, raise that 1st rounding-point from.5 to .7, in order to discourage or prevent splitting-strategy.
BF & HH, in PR, should do the same, for the same reason.
Then, in your example, SL, BF, & HH give one party 0, & give the other party 2.
With single-winner methods, disagreements are often a matter of opinion: “Which problem is more undesirable?”
That isn’t the case in this instance. …& usually isn’t, with PR.
Toby, if you just keep re-asserting your assumptions, instead of even considering what someone is telling you, then you thereby cheat yourself out of the opportunity to find out about the subject.
BTW, a 2-member district is unusual, though there are sometimes such small districts, even in party-list PR.
-
@michaelossipoff OK, I think we can still get to the bottom of this.
Firstly, I see Huntington-Hill as a red herring. Its measure is somewhat arbitrary compared to Sainte-Laguë, despite looking superficially sensible. Huntington-Hill looks at number of seats the parties will get and then looks at the geometric mean, whereas Sainte-Laguë looks at the arithmetic mean. Superficially both might make sense. But with Sainte-Laguë you can look at the representation per voter (rather than seats per party), which is what makes more sense (as it is about giving voters, not parties, representation), and it minimises the variance of that. It is also more generally accepted I believe that Sainte-Laguë gives the closest to exact proportionality possible (I can find sources if need be).
The example I gave was just one example, but it was indicative of what the "Bias Free" method (or indeed any non-Sainte-Laguë method) can do. In any exact tie case under Sainte-Laguë (not just the example I gave), "Bias Free" will award in favour of the smaller party. I see that as systematic bias.
As for what I was talking about with assumptions about distributions, according to Warren Smith's page here:
As our starting point, we shall assume the state populations are independent identically distributed exponential random variables
Is this not the assumption you are making about the distribution?
But the point is that even if under real life conditions, Sainte-Laguë does award larger parties more seats than they are entitled to on average, it is still doing so by using the objectively most proportional method. The bias is not in the method, but what you get from the distribution.
I don't think it makes sense to use a less proportional method to balance this out. If party A and party B are big parties, with C and D small parties, is it better to have one of each over-represented rather than both small or both large represented? I would argue not, because the parties are all separate from each other. It's not small v large, but A v B v C v D.
-
@toby-pereira said in What level of PR do different systems get?:
It is also more generally accepted I believe that Sainte-Laguë gives the closest to exact proportionality possible (I can find sources if need be).
There's a lot of literature on this, but there's just no single "best" PR system. They all optimize different measures of misrepresentation. Huntington-Hill does better on some metrics and worse on others.
Any sensible rule (Dean, HH, Webster, identric) will give almost identical results. The only real discussions are:
- Jefferson (less strategy) vs. everything else (more proportional), and
- Trying "something weird" like varying house sizes (I haven't seen enough research on this, TBH) or fractional votes. Variable house sizes seem like the "least weird" thing you could do here.
I'd suggest picking a house size where the HH+Webster apportionments agree, or using the Webster technique and ignoring the house size constraint (pick a divisor and then round, without updating the divisor). This "does the impossible" (quota and strong monotonicity: every party's number of seats depends only on their vote count, not on the vote counts of other parties; Balinsky-Young theorem assumes a fixed house size).
-
@lime It's not that I'm saying there is a "best" method, but that Sainte-Laguë/Webster is most accurate in terms of pure PR. Other methods might still have certain advantages.
Another thing about Huntington-Hill is that it breaks if a party with any votes has zero seats. It's clearly not the "right" measure.
-
@toby-pereira said in What level of PR do different systems get?:
[quote]
@michaelossipoff OK, I think we can still get to the bottom of this.
[\quote]No, it’s now evident that that was a hopeless cause.
Firstly, I see Huntington-Hill as a red herring. Its measure is somewhat arbitrary compared to Sainte-Laguë, despite looking superficially sensible.
It’s too bad that you weren’t there to set PhD mathematician Huntington straight, & explain to him where he was wrong when he thought he was minimizing variation in s/v !
[quote]
Huntington-Hill looks at number of seats the parties will get…
[\quote]Hello? All allocation-rules are about how many seats a party (or state) will get.
Most of the divisor-methods use a mean as their rounding-point. Arithmetical, geometric, identric, harmonic.
[quote]
and then looks at the geometric mean, whereas Sainte-Laguë looks at the arithmetic mean.Superficially both might make sense. But with Sainte-Laguë you can look at the representation per voter (rather than seats per party)
[\quote] If you’d actually looked at Huntington’s article, as I suggested, you’d find that he was talking about minimizing variation in s/v. He wasn’t trying to make seats per state equal
If you’d actually looked at Huntington’s article, as I suggested, you’d find that he was talking about minimizing variation in s/v. He wasn’t trying to make seats per state equal 
which is what makes more sense (as it is about giving voters, not parties, representation), and it minimises the variance of that. It is also more generally accepted I believe that Sainte-Laguë gives the closest to exact proportionality possible (I can find sources if need be).
For at least the 4th time, HH minimizes variation measured in ratio of s/v values, while SL minimizes variation measured in difference of s/v values.
I don’t know where you get your latest notion, but both minimizations are about s/v.
[quote]
The example I gave was just one example, but it was indicative of what the "Bias Free" method (or indeed any non-Sainte-Laguë method) can do. In any exact tie case under Sainte-Laguë (not just the example I gave), "Bias Free" will award in favour of the smaller party. I see that as systematic bias.
[\quote]Then you see it wrong.
From an assumption that SL is unbiased, then that must mean that to differ from SL is to be biased

[quote]
As for what I was talking about with assumptions about distributions, according to Warren Smith's page here:
[\quote]A morass of gibberish. Warren expounded & theorized about the distribution of the populations of the U.S. states, & felt that it was necessary to base an allocation-rule on such a theory.
I’ve never heard of anyone agreeing with him on that.
At least two academic journal-paper authors agree about BF. I posted reference to two such papers in my September’23 EM posts. One of the authors referred to BF as the Ossipoff-Agnew method.
(Agnew independently proposed the use of the identric mean as the rounding-point of an unbiased divisor-method a few years after I did.)
At the time that I proposed BF in 2006, I hadn’t heard of the identric mean. I determined the average s/v over all the possible numbers of quotas that a party could have in an a-to-b interval, with a given rounding-point. …& solved for the rounding-point that would make that average equal in the various intervals.
I was surprised to hear that that mean had a name, & had been discussed a lot in connection with other matters.
As our starting point, we shall assume the state populations are independent identically distributed exponential random variables
Is this not the assumption you are making about the distribution?
No, that’s Warren.
[quote]
But the point is that even if under real life conditions, Sainte-Laguë does award larger parties more seats than they are entitled to on average, it is still doing so by using the objectively most proportional method.
[\quote]For about the 7th time:
-
SL & HH differ in regards to how they measure variation in s/v. Huntington gives good reasons why his measure (ratio) is more meaningful. I referred you to his article. His use of ratio seems more meaningful to me, because s/v, itself is a ratio.
-
Variation in s/v, & bias are two separate matters. Their minimizations are separate goals.
s/v variation is inevitable. It’s small & unproblematic for divisor-methods. What’s problematic, because it’s an unfair SYSTEMATIC & CONSISTENT inequality, is bias.
Yes, HH goes wrong when it gives a seat to a party with one vote, but Huntington’s argument that HH best minimizes variation in s/v is more convincing than the claim that difference is the meaningful measure.
[quote]
The bias is not in the method, but what you get from the distribution.
[/quote]Nearly all allocation rules have their intrinsic bias. It’s a property of an allocation rule. Perhaps you’ve been listening to Warren. You make far too many careless assertions.
[quote]
I don't think it makes sense to use a less proportional method to balance this out.
[/quote]Suit yourself, & feel free to try to convince people that small random variation is more important than systematic consistent disfavoring.
[quote]
If party A and party B are big parties, with C and D small parties, is it better to have one of each over-represented rather than both small or both large represented? I would argue not, because the parties are all separate from each other. It's not small v large, but A v B v C v D.
[/quote]I have no idea what that means, but it has now become particularly evident that this conversation isn’t accomplishing any purpose.
It obviously isn’t helping you. I often reply to erroneous posts so that they won’t deceive others, but this could obviously go on forever.
I’m done with this conversation.
-