Fun Visual
-
Hey all, just thought I'd share some stuff.
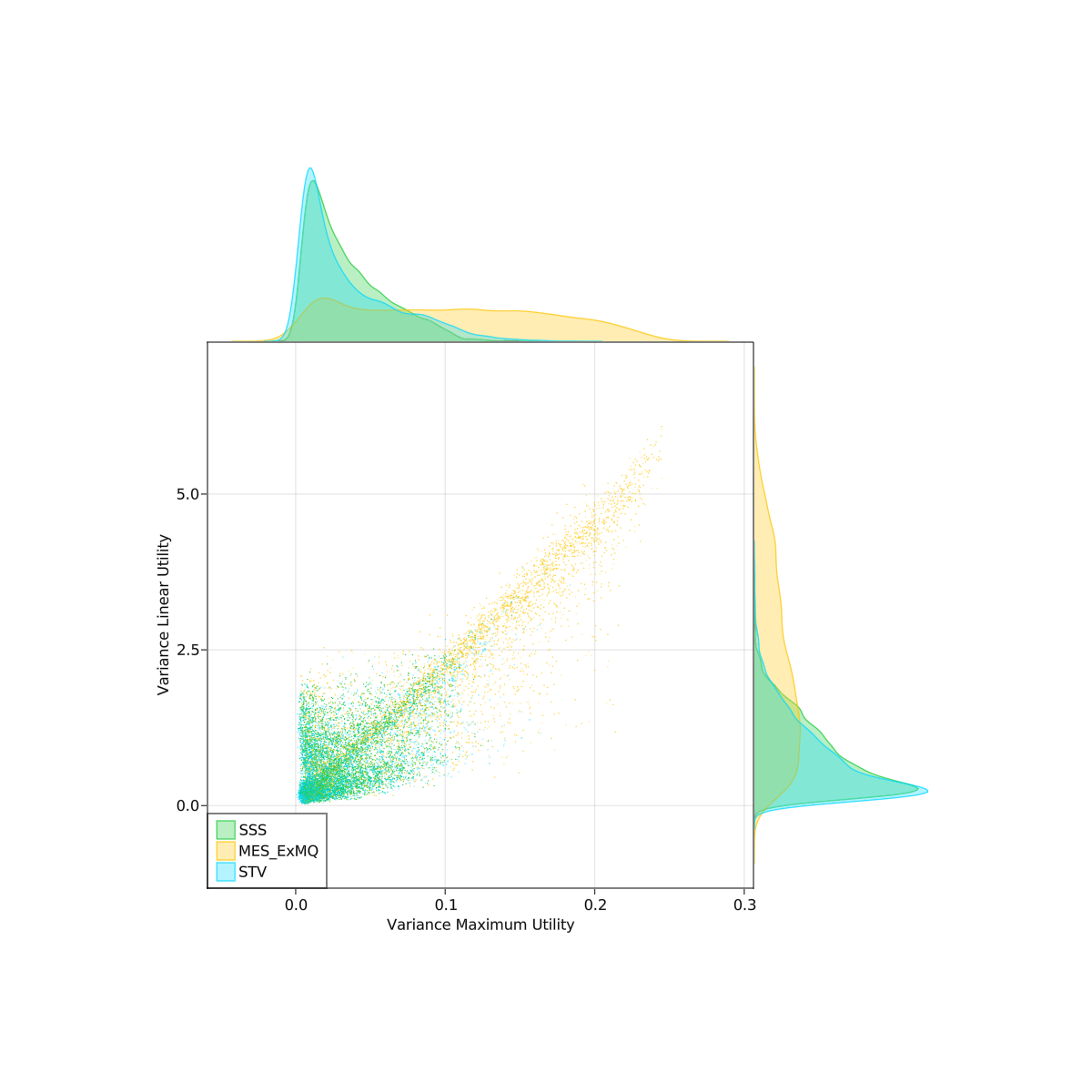
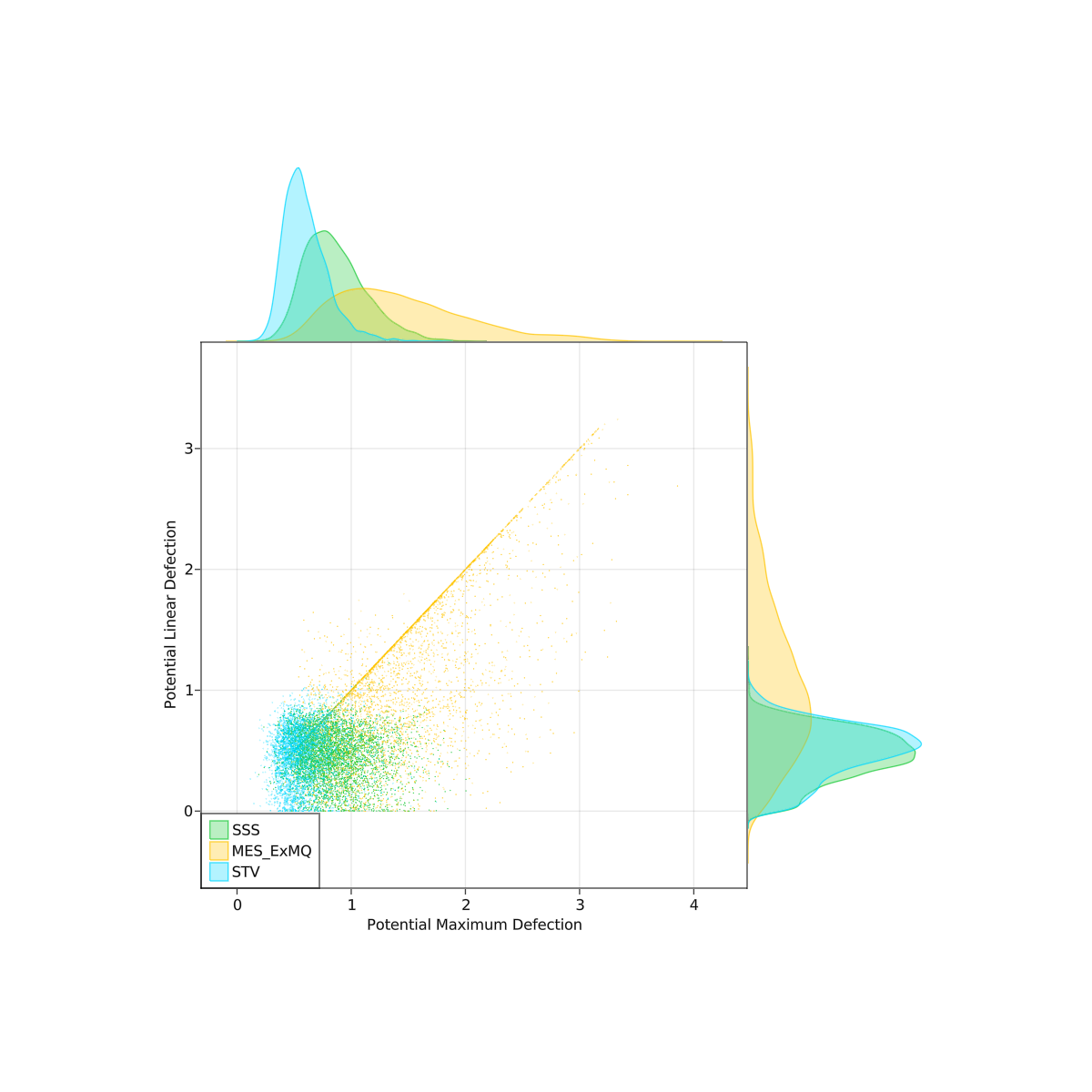
I did some spatial simulations comparing a couple PR rules. It was 2d, gaussian blobs for parties. Randomly chose 2-5 parties, locations, and standard deviations. Each party also had a "disposition" parameter controlling how quickly their utility dropped off with distance. I hand tuned some of the parameters to try to make it more realistic (or at least plausibly so). No guarantee that this model matches reality though, so take these with a grain of salt. The scatterplots below are over 4000 trials.
Methods tested: SSS, MES (with a custom exhaustiveness, but this part didn't make a big difference), and STV. Droop quota was used for all. I also tested AS but I realized I had a bug in the implementation after I ran the experiment.
Linear utility is expected u_i(W) where u_i(W) = sum(u_i(c) for c in W)
Maximum utility is expected u_i(W) where u_i(W) = max(u_i(c) for c in W)
The 'defection' is testing core stability with respect to one-quota and two-quota deviations, with linear and maximum denoting extending utility functions to linear and maximum utilities over sets of candidates.
I also had a strategic % parameter which was chosen from 0-100% for each election, controlling how many voters behaved strategically. For lack of a better strategy, I used what I am calling "Frontrunner Bullets." The election is run on sincere ballots, and the winners are "frontrunners." I assume voters somehow have clairvoyant access to the frontrunners. They then min-max utilities approving all candidates more than average utility awarded to the frontrunners.
I will let you mostly make your own conclusions from the charts.
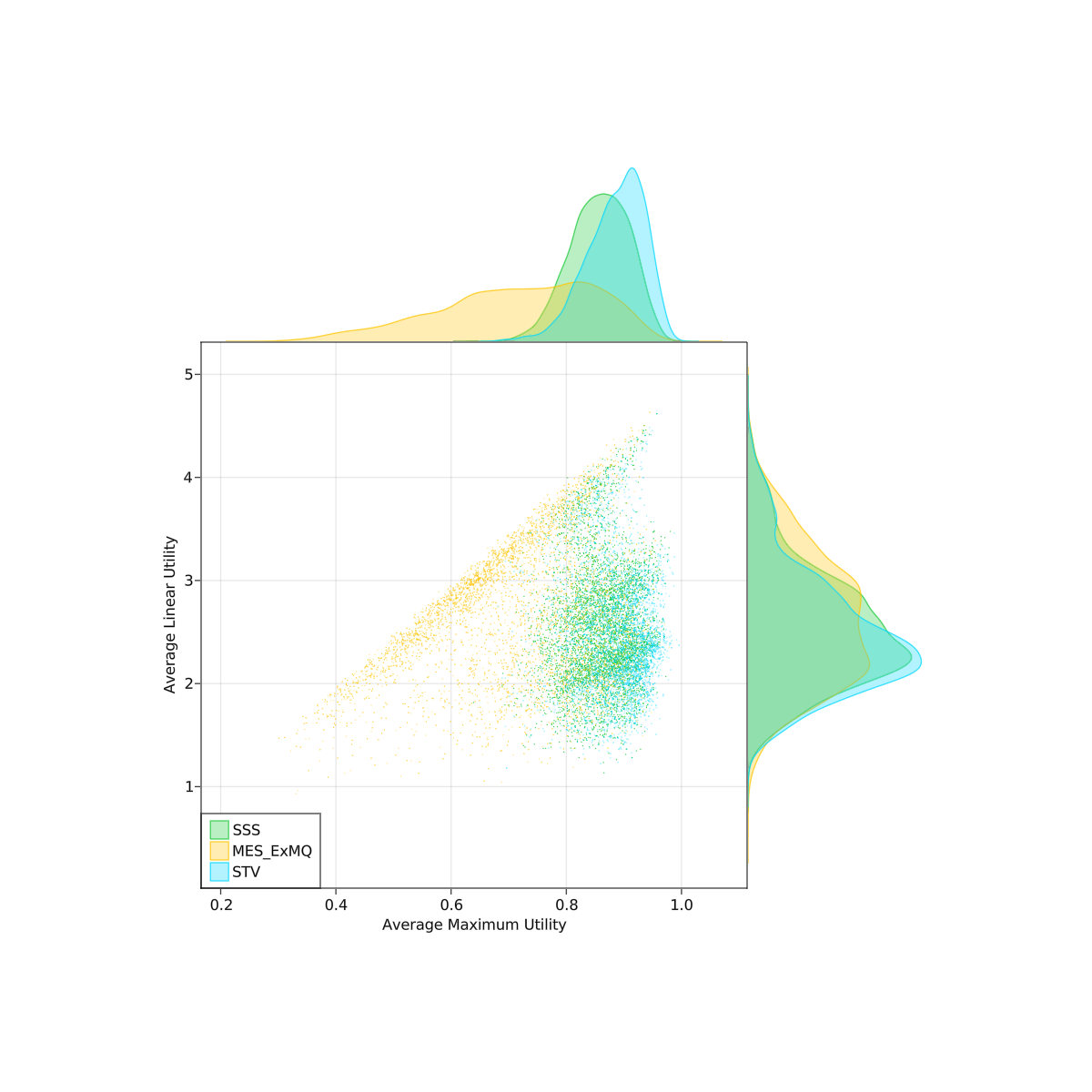
Was interested to see that all the methods converged to more or less the same value with strategic behavior. It was a pretty common pattern that performance would degrade as strategic percentage grows... with the exception of STV, which often got better with strategy. Although, it should be noted I am using a pretty non-standard form of STV where equal ranks are allowed and the voting power is split evenly among candidates at that rank.
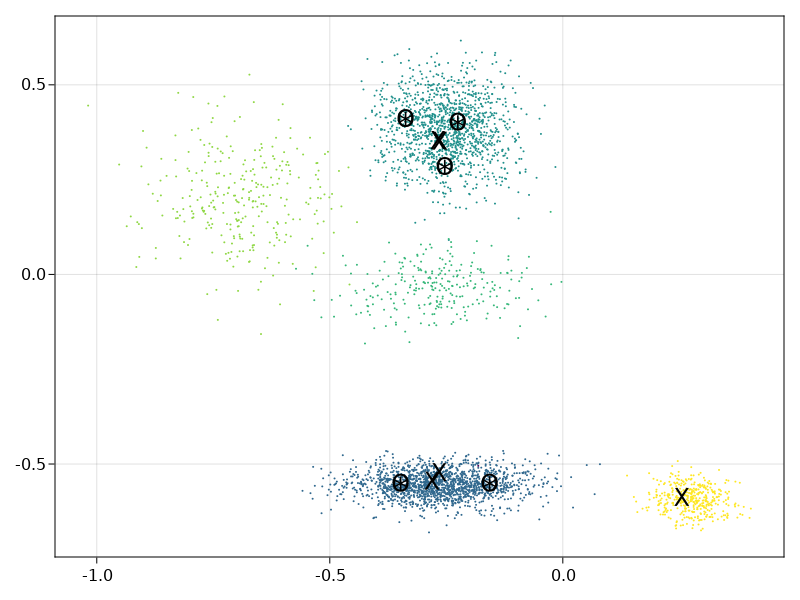
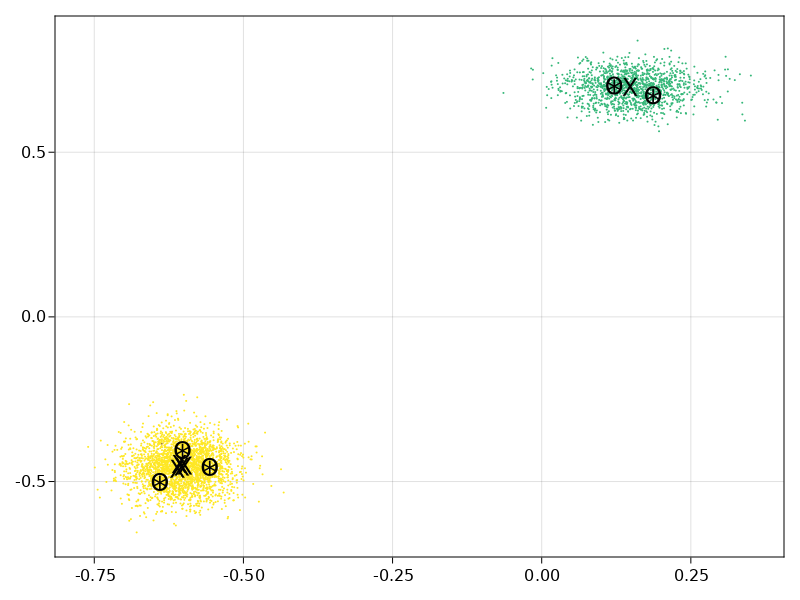
These are just visualizing the choices of winners themselves. Each blob is a party. The "X" are MES winners, "O" are SSS winners, and "*" are STV winners. Sorry I didn't include one where SSS and STV differ. I made this pretty late last night.
-
@andy-dienes I would not expect MES to be so different. Are you sure you do not have a bug.
In any case this is interesting. SSS and STV are very similar in outcome. I realize this is an improved version of STV which makes is closer to SSS but it is likely still susceptible to all the known flaws of STV.
One request, can you please chose a more boring colour colour palette to help us colour blind people. I typically use
['b','r','#FFFF00','g','#808080','#56B4E9','#FF7F00']
-
It is always possible I have a bug, but I did just end up using the implementation on Wikipedia. I think another reason for the poor performance of MES could very easily be due to the utility model. Right now I have it set up so 'neutral' is approximately 0.5 and anything near 0 is 'strong dislike.' MES seems to perform comparatively a lot better when 0 is 'neutral' and anything above 0 is treated as an approval.
Sorry about the colors. Julia's plotting capabilities are still not totally stable so I was having trouble with custom palettes. I will make sure to get that sorted before posting any more.
EDIT: there was indeed a bug, oops. I should write some test cases.
-
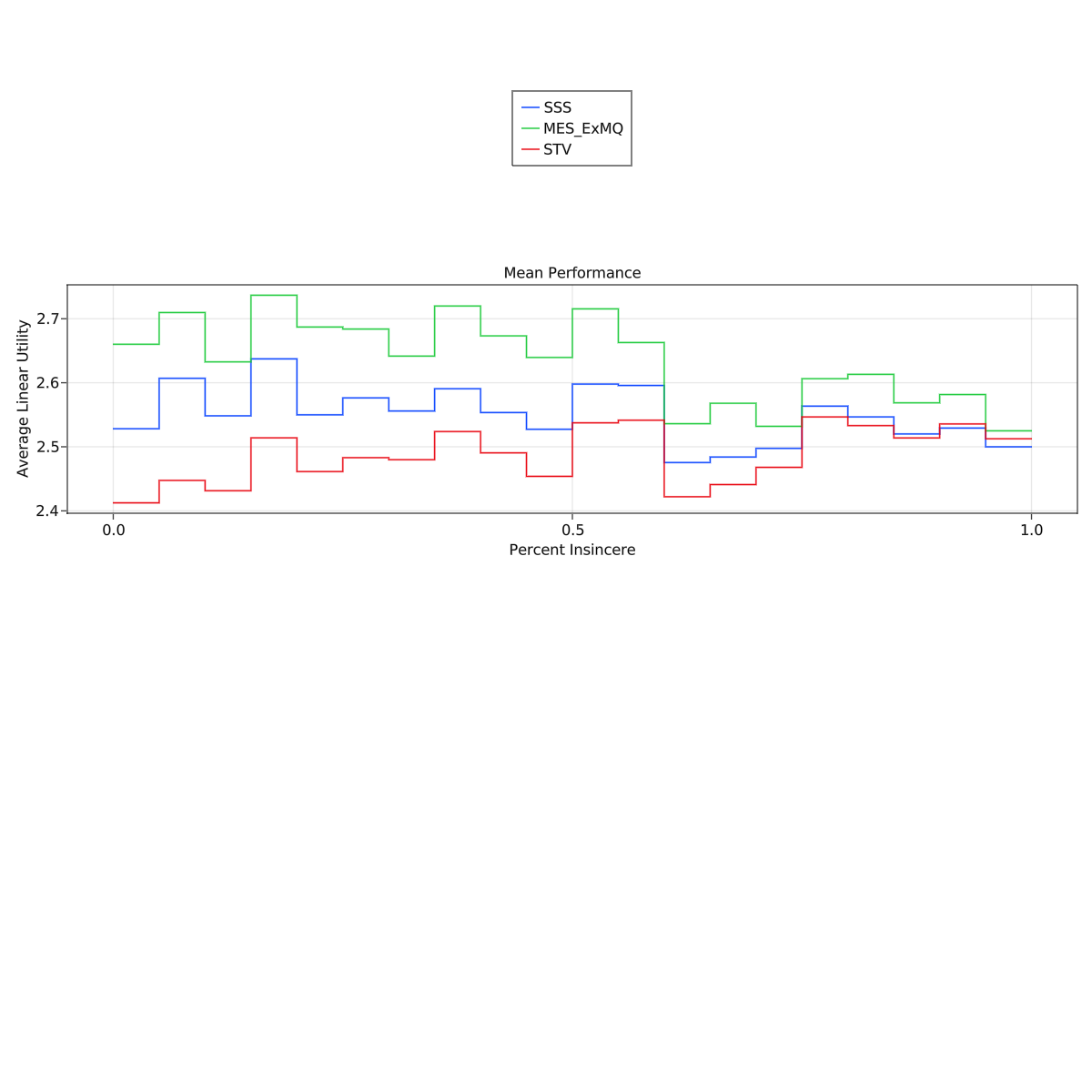
Ok, I tracked down all the bugs and tuned a few more parameters. Here is a summary of the results
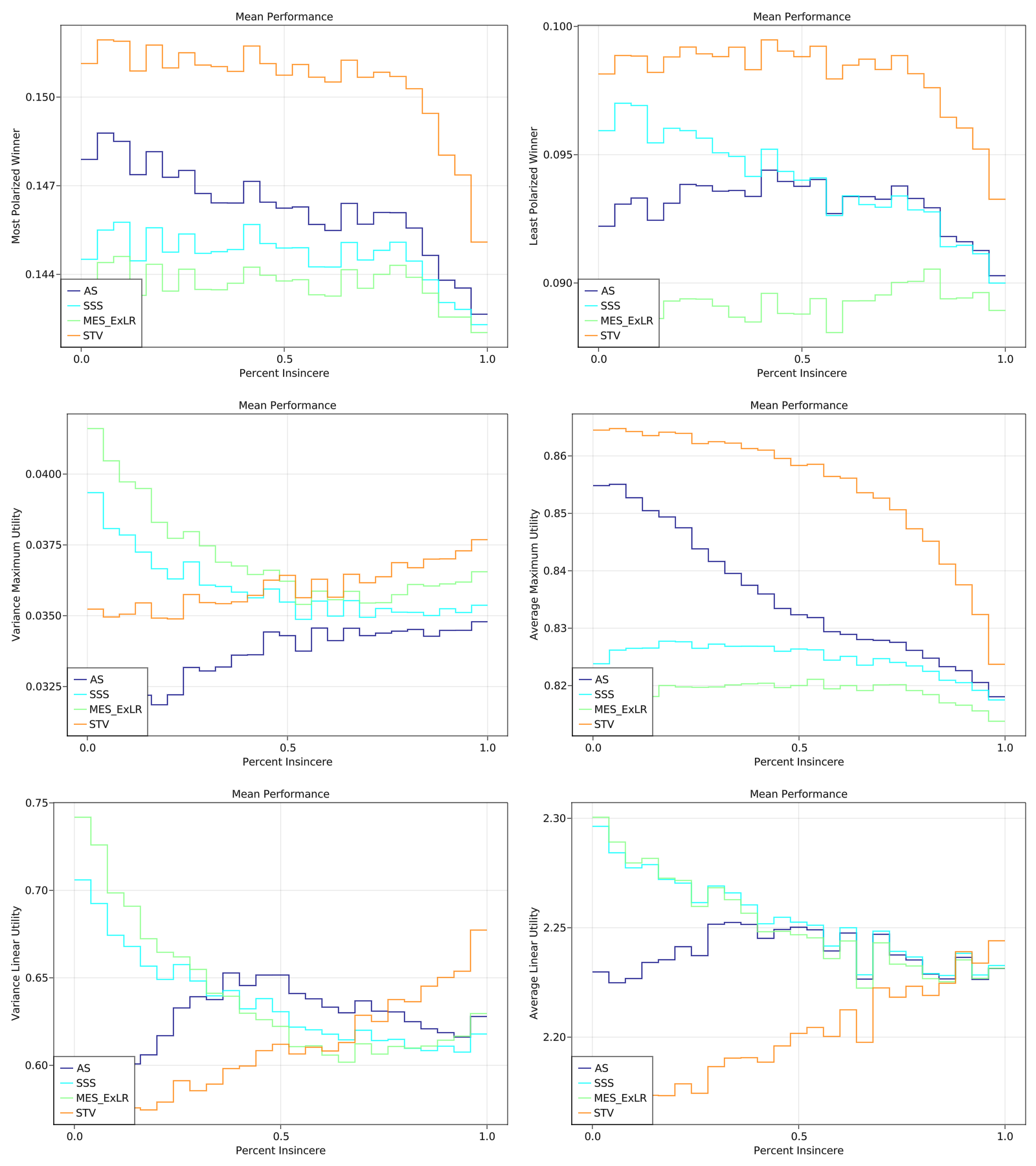
Pay attention to the y-axis bounds---the results were universally pretty similar for every method (suggesting there was usually an obvious set of winners) so the big gaps in the charts are not always that big numerically.
Notably, MES performed significantly better after fixing the implementation issues.
I used colors from a colorblind palette, but it still looks a little funky to me. If they are hard to decipher I can reupload with another palette.
In my eyes, if you expect voters to be at most around 50% "strategic" (although I have only used one type of strategy in these simulations), then AS, SSS, and MES all outperform STV (except for the metric "Maximum Utility"), but among the three there are real tradeoffs.
-
@andy-dienes This is very interesting Andy. It is similar to the conclusions we got from the original simulations which did not include strategy. By this I mean that there was a clear trade off between desirable things. We decided that this trade-off would be skewed by the strategic considerations so it was hard to choose which was best without that. We were using the term Pareto Frontier to refer to this set of trade-offs. I suspect that since the set of choices is a small number of models not a continuously variable property there is a solution which is "best".
About the interpretation, the original simulations where a histogram of the number of simulated elections showing each property. Yours show the mean (?) of each property by the % of strategy. The difference in shape of histogram was important. Particularly if you look at things like "fully satisfied voters" for allocation methods. There are a few ways to solve this. The most obvious is a 2d histogram with the axes of percent insincere and the metric in question. This would prohibit the ability to show multiple models at the same time. The other is to show different metrics other than the mean. You could for example show the standard deviation as an error bar on each point. This would also give you an idea of if the differences are "large". Note that this is not the same as if they are "significant".
For that you would need the standard error on the mean. Judging by the fluctuations between bins you seem to have run about the right amount of simulations needed to distinguish so that is likely not an issue.
To see if things like the "fully satisfied voters" goes away with strategy I would just choose a few points on the percent insincere line and make the same plots as in the original simulations. eg 0%, 25%, 50% and 75%. If the histogram shape is the same at each point then you do not need to dig deeper. I hope this makes sense