Rule X extended to score ballots
-
@toby-pereira said in Rule X extended to score ballots:
When you gave the results for your example in the post a few above you said RRV, but do you mean that you actually used SDV? Edit - In any case I don't think RRV is the method worth calculating results for.
It was RRV. The only good thing about RRV is that it is simple to calculate. It was included to be illustrative. I think STV is garbage but I included that too as a reference point. I think DSV is the best Thiele system but I do not like Thiele systems so I never bothered to code it.
@toby-pereira said in Rule X extended to score ballots:
Yeah, that's the one that's SPAV + KP, right? I think that's still my preferred Thiele-based option.
Yes that is what it is called on this page. https://electowiki.org/wiki/Kotze-Pereira_transformation
There is no proper page for it. If you want to advocate for it you should make one
-
@keith-edmonds Also if we don't include RRV, people who learn about some of this stuff through scorevoting.net might read the report and ask, "where's RRV?"
If we didn't include STV, we'd have the same problem, just with different entry points.
-
@marylander said in Rule X extended to score ballots:
through scorevoting.net
That url makes me shudder ...
-
Just to add---I also now computed the var-Phragmen objective for each of those committees. It is a bit slower since it is a nonlinear objective so I only did 400 trials not 1000.
but the results are:
AAABC: 0.00018
ABBBB: 0.247
AAABB: 0.186
AAACC: 0.00042
AABBC: 0.00011For context, the var-Phragmen objective tries to minimize the variance of the 'voter load.' It is equivalent to Sainte-Lague when voters vote along party-lists. There is a stripped-down (much easier to compute but less useful information) version of this metric sometimes referred to as 'Ebert cost.'
-
@keith-edmonds said in Rule X extended to score ballots:
Consider this 5 winner example with clones for each candidate
Red: 61% vote A:5, B:3, C:0
Blue: 39% vote A:0, B:3, C:5RRV Gives ['A1', 'C1', 'A2', 'B1', 'B2']
MES Gives ['A1', 'A2', 'A3', 'C1', 'B1']
SSS Gives ['A1', 'B1', 'B2', 'B3', 'B4']
Allocated score Gives ['A1', 'B1', 'A2', 'B2', 'A3']
STV Gives ['A1', 'A2', 'A3', 'C1', 'C2']I could have made a calculational error but I did it with code which I can post if people want to look for bugs. If correct this is super interesting. They all give different results.
Which sets are in the core? If any?
Just out of interest, I worked this out with COWPEA + KP and got the following percentages (assuming I calculated correctly):
A: 43.1%
B: 34.3%
C : 22.6%This would probably mean 2 As, 2Bs and a C in a five-seat constituency (the RRV result). Which I think you consider to be not a great result.
-
@Toby-Pereira I think you may be interested in the notion of "Individual Representation" (IR) here
https://arxiv.org/abs/2112.05193
It is basically the same kind of idea of Justified Representation, but made about as strong as it gets.
It requires that every voter who is part of an f-cohesive group must have at least f winners in the committee. I think this is a cool thing to consider because
- On the surface, it sounds very desirable (although it is not always possible).
- Like the notion of "balanced stable priceability" (BSP, a tweak on core stability) it is in some sense the strongest possible demand for a certain philosophy on proportionality
- Despite the above two, it is strongly incompatible with core stability in that there is an election where the committees providing core-stability (and thus also any BSP committee) is disjoint from the set of committees providing IR.
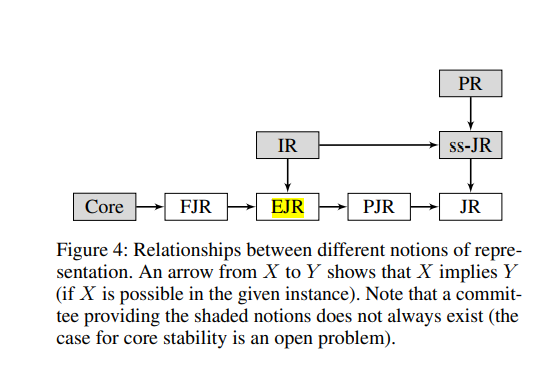
edit: I know this is a lot of acronyms so I'll provide a synopsis for those who don't have as much time to waste reading papers as I do:
Say 5 quotas of voter (say, S) all agree on 5 candidates (say, T). Then
- Justified Representation (JR) says at least one voter in S should approve at least one winner
- semi-strong JR says every voter within S should approve at least one winner
- strong JR says one of the candidates in T needs to win
- Proportional JR (PJR) says the voters in S need to approve at least 5 winners total
- Extended JR (EJR) says at least one voter in S needs to approve at least 5 winners total
- Fully JR (FJR) is the same as EJR with a fractional relaxation of the definition of 'cohesive,' so if instead of unanimity we have 5 quotas of voters S all approve 3 out of some set of 5 candidates T, then at least one voter in S approves at least 3 winners.
- Individual Representation (IR) says every voter in S needs to approve at least 5 winners total
In this light, you might think of IR as semi-strong EJR. I'm sure you could also define strong EJR (i.e., all candidates in T need to win) but this would be an incredibly restrictive criterion. Interestingly, you could also define FJR with a PJR flavor (voters from S approve at least 3 winners total), or semi-strong (voters from S approve at least 3 candidates each) or strong (3 candidates from T are elected). I haven't seen these notions in the literature yet and I'm not really sure how they would compare to the other ideas, but it's definitely on theme.
Core, BSP, and PR are defined in other ways that are not as easy to summarize, but here's a shot at it:
- a committee W is core if there is no coalition of voters S comprising at least f quotas, and can propose f winners T such that all of S prefers T to W
- BSP means voters can be fractionally assigned to winners they support in W such that every winner gets the same total ballot weight assigned, each voter assigned to that winner spends the same fraction of ballot weight, no coalition has enough remaining support to elect a non-winner, and it is stable in the core sense.
- Perfect Representation (PR) means that voters can be partitioned into quotas such that each quota is unanimous for a winner.
Now, the incompatibilities above mean that it will be impossible to satisfy all of these criteria in every circumstance... but there may very well be an algorithm out there that either simutaneously approximates BSP & IR, or one that is guaranteed to provide either an IR or a BSP committee, when at least one exists. Of course if neither exists then who knows what the right committee is, but I think here there be dragons.
-
@andy-dienes Its worth considering that the extension of JR to score could have been done differently and it is not clear what Piotr did was correct.
For example, the SSS can fail this version of JR because a group does not agree on full support for any candidate. It comes from the extension of JR to score. I think of PR in the score case more like how using the Kotze-Pereira transformation then approval JR works. You need a quota of voters giving full support or 2 quotas giving half support. I think in terms of quotas of score not quotas of voters.
MES allows a voter to buy a candidate for more than their score/utility given on the ballot if rho >0. This violates what I call Vote unitarity. What would MES do if you limited rho to be less than 1? That would be much more similar to SSS but might be broken. Consider the pathological scenario for MES.
Candidates = ['A','B1','B2','B3','B4','B5','B6']
1 * [[1,5,0,0,0,0,0]]
5 * [[1,0,5,0,0,0,0]]
5 * [[1,0,0,5,0,0,0]]
5 * [[0,0,0,0,5,0,0]]
5 * [[0,0,0,0,0,5,4]]
5 * [[0,0,0,0,0,3,5]]Winners = 5.0
I submit that A should not be elected but MES selects it. This is not an unrealistic example either. Allocated score can do similar things. It comes from the sort and I have long complained about whole ballots being allocated for a score of 1. For the MES case it is related to candidates being just short of a full quota.
A related issues with MES is that it needs a completion method and they chose bloc score. I think SSS would be a better "completion method" for MES instead. It would avoid situations like
['A','B1','B2','B3','B4','B5','C0','C1','C2']
39 * [[0,5,5,5,5,5,0,0,0]]
18 * [[0,0,0,0,0,0,5,0,0]]
17 * [[0,0,0,0,0,0,0,5,0]]
16 * [[0,0,0,0,0,0,0,0,5]]
7 * [[5,0,0,0,0,0,0,0,0]]
2 * [[5,0,0,0,0,0,0,0,0]]Winners = 5.0
MES returns ['B1','B2','B3','B4','B5'] but with the SSS completion you get ['B1', 'B2', 'C0', 'C1', 'C2'].
Anyway, single examples are not really great since all systems have problems. We need to simulate the three with strategy.
-
One criterion that I would regard as essential for any approval-based proportional method is that in the case where the number of candidates equals the number of voters, then if the ballots make it possible for each voter to be uniquely assigned a candidate that they approved, then such a result must be the result.
It's a bit like perfect representation, except that perfect representation makes the demand for fractions of candidates. (E.g. if it's possible for each voter to be assigned their own unique 0.05 of a candidate - allowing e.g. for 0.025 each for two candidates - then this must happen.)
A similar criterion would be that for each new candidate you add to the committee from 1 upwards, they must be assignable to a different voter, until every voter has their own candidate (assuming the ballots make it possible). It would then continue with each voter getting a second candidate in turn if even more candidates were added.
Thiele-based methods fail this.
-
Perhaps this deserves its own thread but I will just put it here for now:
Here is a proposed proportionality criterion possibly satisfied by SSS (and if so, probably MES as well). It intends to look at proportionality of utility rather than proportionality of ballot weight. I have adapted slightly the definition of FJR to make it more PJR-like as I explained in my prior post. I think the partial cohesion framework makes a lot of sense to use when talking about proportionality of utility.
Say there is a coalition of voters S such that |S| is at least M quotas. Say for (integer) beta <= M that there is a set T of M candidates such that u_i(T) >= beta for all i in S. Then for any winning committee W, it must be satisfied that sum_{c in W} max_{i in S} u_i(c) >= beta.
Note that this is still a rather weak condition and does not guarantee utility-efficient committees. One way to strengthen it might just be to use FJR and instead demand that max_{i \in S} u_i(W) >= beta.
Is either criterion satisfied by SSS or MES? Any quick counter-examples?
Edit:
Please feel free to check my arithmetic, but I believe this example shows that MES satisfies neither criterion above, even when it is exhaustive and does not return early. This is obviously a pathological scenario, but nonetheless it is one where MES returns clearly the 'wrong' result.5 candidates (A, B, C, D, E). 3 to elect. Quotas give scores
q_1: (1, 0, 0.01, 0.01, 0.01)
q_2: (0, 1, 0.01, 0.01, 0.01)
q_3: (0, 0, 1, 1, 1)Since every voter in the coalition of quotas q_1 and q_2 gets utility 1 from {A, B}, then the criterion would demand that at least one voter gets utility 1 from the winning committee (alternatively, the weaker condition that the sum of max utilities in the coalition for the winning candidates is 1).
Round 1
Ballot weights: q_1 = 1, q_2 = 1, q_3 = 1
elect C for a price of 50/51Round 2
Ballot weights: q_1 = 101/102, q_2 = 101/102, q_3 = 1/51
elect D for a price of 2500/51 (around 49.02)Round 3
Ballot weights: q_1 = 1/2, q_2 = 1/2, q_3 = 0
elect E for a price of 50So the winning set is {C, D, E}. The utility of any voter in q_1 or q_2 is 0.03, far short of 1, so the criterion is violated. On the other hand, SSS, AS, STV all return {A, B, C}, the 'correct' winner set.
Unfortunately, it's not true for SSS either. Consider the example where there are 2 voters and two candidates to elect. Voter 1 submits (1, 0.99, 0) and voter 2 submits (0, 0.011, 1).
-
@keith-edmonds Just tested my implementation of MES and it gets the same results as you state for SSS, on these two examples.
-
@Ted-Stern Are you referring to this?
Consider this 5 winner example with clones for each candidate
Red: 61% vote A:5, B:3, C:0
Blue: 39% vote A:0, B:3, C:5
RRV Gives ['A1', 'C1', 'A2', 'B1', 'B2']
MES Gives ['A1', 'A2', 'A3', 'C1', 'B1']
SSS Gives ['A1', 'B1', 'B2', 'B3', 'B4']
Allocated score Gives ['A1', 'B1', 'A2', 'B2', 'A3']
STV Gives ['A1', 'A2', 'A3', 'C1', 'C2']The code I ran (which I can share) was taken from the electowiki page written by the inventor Piotr Skowron and I confirmed with him personally that the result was correct. I suspect you have a bug.