Paradox of Causality from Arrow’s Impossibility Theorem
-
Well, aside from that, I think Arrow's Theorem is overstated in terms of its importance anyway. Pretty much all ranked-ballot methods fail IIA and if they don't they are unreasonable in some other manner. This has been known for ages anyway as it is a logical consequence of the Condorcet paradox.
So Arrow's Theorem was no great paradigm shift in our understanding. It's a non-event if you ask me.
-
@toby-pereira said in Paradox of Identity in the Proof of Arrow's Impossibility Theorem: the existence of a “Dictator” is Non-constructive:
I think Arrow's Theorem is overstated in terms of its importance anyway.
Yup. To me it's "importance" is in slowing down progress and adoption of better methods....
I compared it in another thread to the proof that you can't express Pi as a decimal. It's technically true, but given that there is no limit to how close you can come ( https://techxplore.com/news/2019-03-pi-trillion-decimals-google-day.html ), it would be stupid to use it to argue that any calculations that rely on a decimal representation of Pi are unreliable.
Same thing here. Arrow (and Gibbard) are red herrings, when it comes to practical mechanisms for resolving group decisions.
-
Kenneth Arrow absolutely deserved his Nobel Prize, because Arrow's Theorem was (and is) a big deal. The exact choice of criteria was beside the point; what Arrow did was describe a few "common sense" criteria and then showed them to be mutually exclusive. Later work (e.g. Gibbard-Satterthwaite) had more compelling criteria, but his description (and proof) of how these criteria can be mutually exclusive keeps us from wasting time when evaluating methods.
The metaphor I frequently use: there's no such thing as a perfect vehicle (infinitely fast, spacious cargo capacity, fits in a backpack, completely safe, high fuel efficiency), However, new vehicles come out every year that are purportedly better than the prior year's vehicles, and there are many old vehicles that don't live up to today's safety and performance standards. First-past-the-post barely lived up to 18th century performance standards (and quickly led to the two-party system that George Washington hoped to avoid by creating a norm against parties. We see how that worked out.
Arrow's Theorem has been turned into an excuse by people touting inferior voting methods ("no system is perfect"), but we should be able to explain why the status quo sucks without trashing Arrow and his work.
-
@robla Yeah I'm not trashing Arrow so much as the people who do what you describe (tout inferior methods and justify it with Arrow and Gibbard).
I do think Arrow and Gibbard have far less relevance to many discussions than many people give them. Note that the "counting criteria" approach is also symptom of the same thing. Basically, it's black and white thinking, which distracts from the non-black and white issues at hand.
Like with your car analogy.... no one complains about a car not being "completely safe", we all recognize that there are circumstances that you can die in a car crash, and that some cars are better than others but none are perfect. If anyone treated that as a binary, most of us would think they were rather clueless.
But when you see this sort of thing:
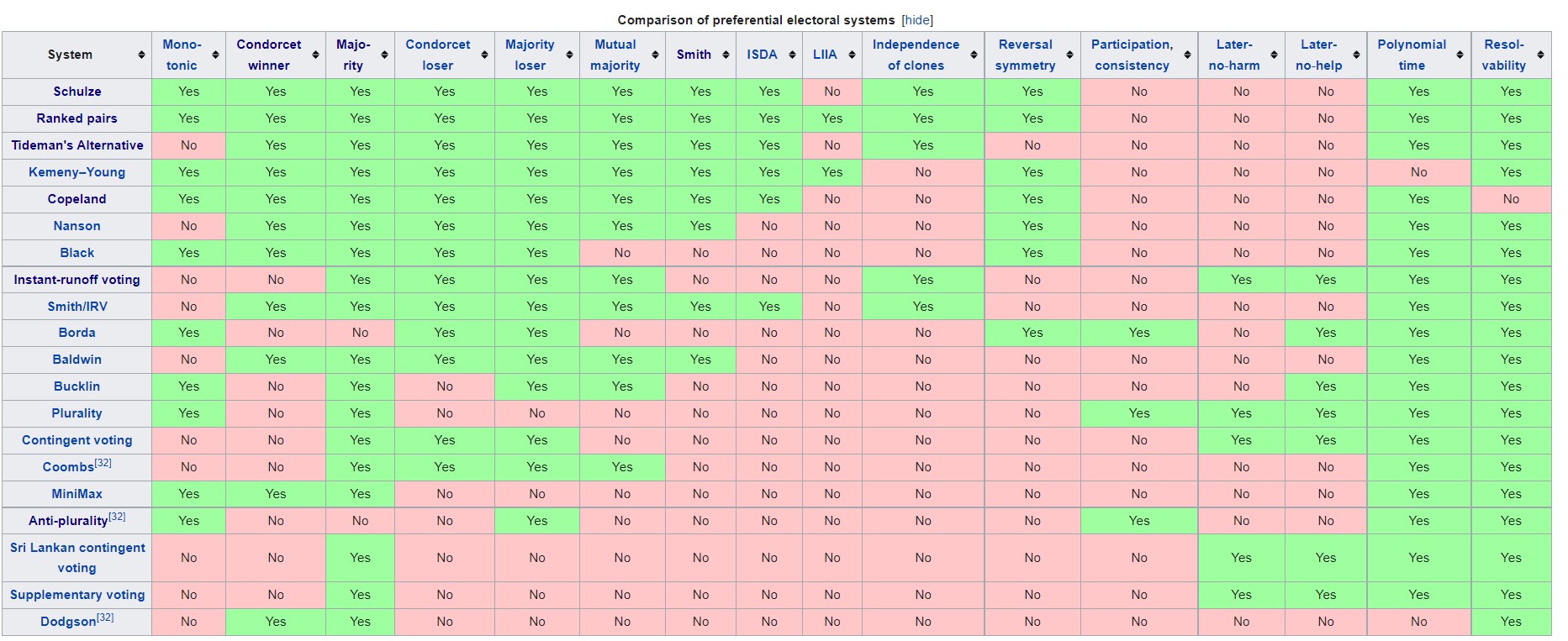
there is a strong implication that the more criteria a method meets, the better, without regard to the degree that a method handles the issue referenced by the criterion. -
@robla said in Paradox of Causality from Arrow’s Impossibility Theorem:
Kenneth Arrow absolutely deserved his Nobel Prize, because Arrow's Theorem was (and is) a big deal. The exact choice of criteria was beside the point; what Arrow did was describe a few "common sense" criteria and then showed them to be mutually exclusive.
But my point is that we already knew that. Amongst Arrow's criteria is IIA. And that's the one that always fails in reasonable methods. It's not like some methds fail this, others fail that. How many methods are there that are just dictatorships, for example? It's IIA all the way. Arrow's Theorem can be reworded in plain English as "With a few reasonable background assumptions, any reasonable ranked-ballot voting method fails IIA." And that has been known for centuries. Arrow just dressed it up differently.
-
@toby-pereira said in Paradox of Causality from Arrow’s Impossibility Theorem:
And that's the one that always fails in reasonable methods
Approval passes IIA but fails universal domain
-
@andy-dienes said in Paradox of Causality from Arrow’s Impossibility Theorem:
@toby-pereira said in Paradox of Causality from Arrow’s Impossibility Theorem:
And that's the one that always fails in reasonable methods
Approval passes IIA but fails universal domain
How exactly did Arrow define universal domain? On the Wikipedia, unrestricted domain is defined as "a property of social welfare functions in which all preferences of all voters (but no other considerations) are allowed", which is a bit vague. What does it mean by all preferences?
Does score fail? What about score that allows any number between the min and max score so that a full preference order can be inferred?
-
@toby-pereira "universal domain" means that the social welfare function is well-defined for all possible (finite) sets of ranked-order ballots, and will always return a total, strict ranking of all of the candidates as its output. Score does not meet the universal domain criterion, since it does not return a strict ranking of all candidates. In particular, it is possible for two candidates to have the same sum of scores, so the score system itself cannot decide on the rank order between those candidates without an additional tie-breaking procedure.
This relaxation of the output structure from strict ranking to a weak ranking is one reason why score procedures are not subject to Arrow's theorem, the other being that the ballots also are not strict rankings. I believe Arrow eventually came to the opinion that social welfare functions are too restrictive and that score ballots without strict rankings would be preferable, possibly since they might be able to satisfy some score-analogs of IIA and Pareto efficiency without becoming dictatorial and probably among other reasons too.
-
@andy-dienes said in Paradox of Causality from Arrow’s Impossibility Theorem:
Approval passes IIA
But only under some (completely nuts) assumptions. For instance, if there are 3 candidates, and I approve Alice and Bob, but not Chris, for it to be independent of irrelevant candidate Chris, they have to assume that I would still approve both Alice and Bob if they were the only candidates. That makes no sense.
-
@rob I'm just going off of the definitions, no assumptions needed

Agreed that voters' ballots will likely change depending on the candidates in the race in Approval more with a higher probability than in most other voting rules.
@Toby-Pereira to answer your question I'm looking into it. Arrow's Theorem actually has quite a few (slightly different) formalizations, and it looks like what I said is technically not true for the version defined on Wikipedia since that one only allows (strict) linear orders, but I feel quite sure I saw a formalization where the domain was all (weak) linear orders. I will try to find it.